Question
Question: $\frac{K_{P_1}}{K_{P_2}}=\frac{(n)^n \cdot P_1^{\Delta \nu_1}}{(m+k)^{(m+k)} \cdot P_2^{\Delta \nu_2...
KP2KP1=(m+k)(m+k)⋅P2Δν2(n)n⋅P1Δν1
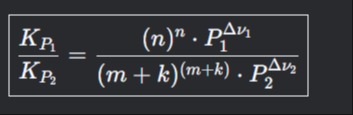
KP2KP1=(m+k)(m+k)⋅P2Δν2(n)n⋅P1Δν1
Solution
The given expression is:
KP2KP1=(m+k)(m+k)⋅P2Δν2(n)n⋅P1Δν1
This equation represents a ratio of two equilibrium constants, KP1 and KP2, for two different chemical reactions or the same reaction under two different sets of conditions (e.g., total pressures P1 and P2).
In this context:
- KP1 and KP2 are the equilibrium constants in terms of partial pressures for reaction 1 and reaction 2, respectively.
- P1 and P2 are the total pressures at which reaction 1 and reaction 2, respectively, reach equilibrium.
- n represents the number of moles of gaseous products formed from one mole of reactant in the first reaction (e.g., if A⇌nB).
- Δν1 (or Δng1) is the change in the number of moles of gaseous products minus gaseous reactants for the first reaction.
- (m+k) represents the number of moles of gaseous products formed from one mole of reactant in the second reaction (e.g., if C⇌mD+kE, then nproducts=m+k).
- Δν2 (or Δng2) is the change in the number of moles of gaseous products minus gaseous reactants for the second reaction.
This specific form of the expression suggests that certain terms related to the degree of dissociation (α) have either cancelled out or are assumed to be constant (e.g., equal to 1) in the derivation of this ratio. It is a formula used to compare equilibrium constants under varying pressures and stoichiometric changes.
The question asks for the solution to the given expression. As it is already an expression representing a relationship, the solution is the expression itself and its interpretation in the context of chemical equilibrium.
No specific numerical answer or simplification is possible without further context or values for the variables.
