Question

$\frac{\Huge\boxed{?}}{a^3}a^{(\log_{10}a^2)}=100$

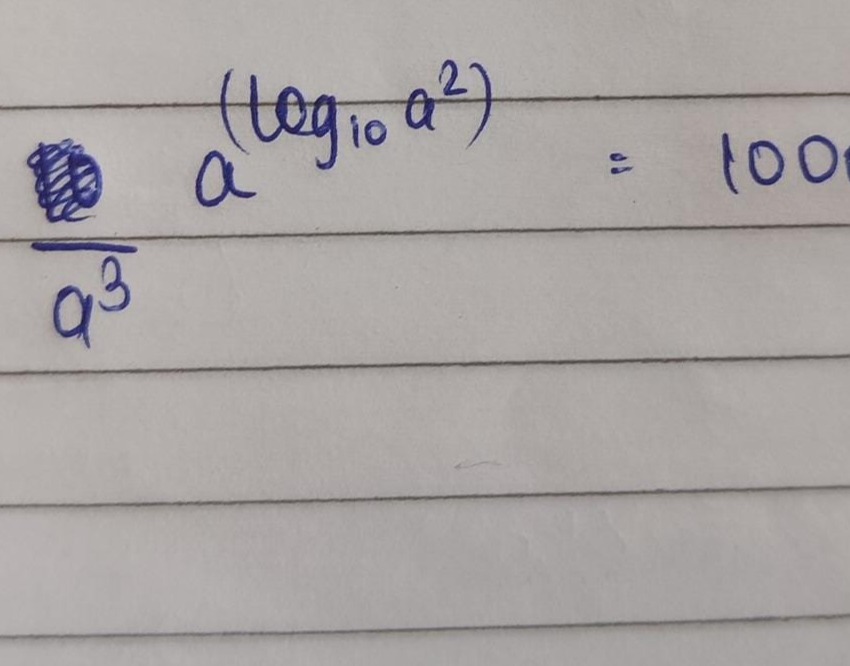
Answer 1

100 * a^(3 - 2*log10(a))

Answer 2

Let the value in the box be $X$. The given equation is:

$$\frac{X}{a^3}a^{(\log_{10}a^2)}=100$$

To find the value of $X$, we can rearrange the equation:

$$X = 100 \times \frac{a^3}{a^{(\log_{10}a^2)}}$$

Using the properties of exponents, $\frac{b^m}{b^n} = b^{m-n}$, we can write:

$$X = 100 \times a^{3 - (\log_{10}a^2)}$$

Using the property of logarithms, $\log_b c^d = d \log_b c$, we have $\log_{10}a^2 = 2\log_{10}a$. Substituting this into the expression for $X$:

$$X = 100 \times a^{3 - 2\log_{10}a}$$

This is the expression for the value in the box.