Question

$\frac{\Huge\boxed{?}}{a^3}a^{(\log_{10}a^2)}=100$

Answer 1

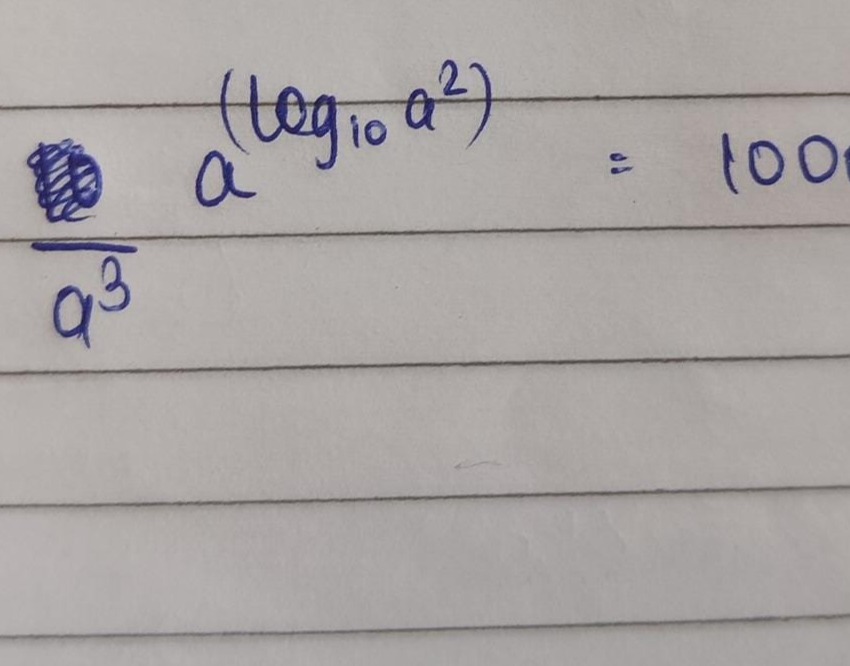
$100 a^{3 - 2\log_{10}a}$

Answer 2

Let the expression in the box be $X$. The given equation is: $\frac{X}{a^3}a^{(\log_{10}a^2)}=100$ We need to solve for $X$. First, let's simplify the term $a^{(\log_{10}a^2)}$. Using the logarithm property $\log_b x^n = n \log_b x$, we have $\log_{10}a^2 = 2 \log_{10}a$. So, the term becomes $a^{(2 \log_{10}a)}$.

Now the equation is: $\frac{X}{a^3}a^{(2 \log_{10}a)}=100$ We can rewrite $a^{(2 \log_{10}a)}$ as $a^{\log_{10}(a^2)}$. Using the property $x^{\log_b y} = y^{\log_b x}$, we can swap the base and the argument of the logarithm. Let $x=a$, $y=a^2$, and $b=10$. $a^{\log_{10}(a^2)} = (a^2)^{\log_{10}a}$ So the equation becomes: $\frac{X}{a^3}(a^2)^{\log_{10}a}=100$ Now, let's express $a$ in terms of base 10 using $a = 10^{\log_{10}a}$. Then $a^2 = (10^{\log_{10}a})^2 = 10^{2\log_{10}a}$. Substitute this into the equation: $\frac{X}{(10^{\log_{10}a})^3} (10^{2\log_{10}a})^{\log_{10}a} = 100$ $\frac{X}{10^{3\log_{10}a}} 10^{(2\log_{10}a)(\log_{10}a)} = 10^2$ $\frac{X}{10^{3\log_{10}a}} 10^{2(\log_{10}a)^2} = 10^2$ Multiply both sides by $10^{3\log_{10}a}$: $X \cdot 10^{2(\log_{10}a)^2} = 10^2 \cdot 10^{3\log_{10}a}$ $X = \frac{10^2 \cdot 10^{3\log_{10}a}}{10^{2(\log_{10}a)^2}}$ Using the property $10^m \cdot 10^n = 10^{m+n}$ and $\frac{10^m}{10^n} = 10^{m-n}$: $X = 10^{2 + 3\log_{10}a - 2(\log_{10}a)^2}$ This is the expression for $X$. Let's try to simplify the exponent. Let $m = \log_{10}a$. The exponent is $2 + 3m - 2m^2$. This does not seem to lead to a simple expression in terms of $a$.

Let's go back to the form $\frac{X}{a^3}(a^2)^{\log_{10}a}=100$. We want to isolate $X$. $X = 100 \cdot a^3 \cdot (a^2)^{-\log_{10}a}$ $X = 100 \cdot a^3 \cdot (a)^{-2\log_{10}a}$ Using the property $a^m \cdot a^n = a^{m+n}$: $X = 100 \cdot a^{3 - 2\log_{10}a}$ This expression is the value in the box. Let's check if this simplifies the original equation when placed in the box. Substitute $X = 100 \cdot a^{3 - 2\log_{10}a}$ into the left side of the original equation: $\frac{100 \cdot a^{3 - 2\log_{10}a}}{a^3}a^{(\log_{10}a^2)}$ $= 100 \cdot a^{3 - 2\log_{10}a - 3} \cdot a^{(2\log_{10}a)}$ $= 100 \cdot a^{-2\log_{10}a} \cdot a^{2\log_{10}a}$ $= 100 \cdot a^{(-2\log_{10}a) + (2\log_{10}a)}$ $= 100 \cdot a^0$ $= 100 \cdot 1 = 100$ This matches the right side of the equation. So the expression in the box is $100 \cdot a^{3 - 2\log_{10}a}$.

We can rewrite $a^{3 - 2\log_{10}a}$ using the property $a^{m-n} = a^m/a^n$: $a^{3 - 2\log_{10}a} = a^3 \cdot a^{-2\log_{10}a} = a^3 \cdot (a^{\log_{10}a})^{-2}$. Let $m = \log_{10}a$. Then $a = 10^m$. $a^m = (10^m)^m = 10^{m^2}$. $a^{-2\log_{10}a} = a^{-\log_{10}a^2}$. Using $x^{\log_b y} = y^{\log_b x}$: $a^{-\log_{10}a^2} = (a^2)^{-\log_{10}a}$. Also, $a^{-2\log_{10}a} = (a^2)^{-\log_{10}a}$. $a^{-2\log_{10}a} = (10^{\log_{10}a})^{-2\log_{10}a} = 10^{-2(\log_{10}a)^2}$.

So, $X = 100 \cdot a^3 \cdot a^{-2\log_{10}a}$. This form $100 a^{3 - 2\log_{10}a}$ is the simplified expression for the content of the box.