Question

$\frac{dy}{dx}=y \tan x - 2 \sin x$

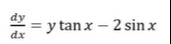
Answer 1

$y = \cos x + K \sec x$

Answer 2

The given differential equation is converted into the standard linear form $\frac{dy}{dx} + P(x)y = Q(x)$. The integrating factor (IF) $e^{\int P(x) dx}$ is calculated. The general solution $y \times IF = \int (Q(x) \times IF) dx + C$ is then applied, and the resulting integral is evaluated using trigonometric identities. Finally, the equation is solved for $y$.