Question

$\frac{dy}{dx} + \frac{x}{x}y = y^2 \ln x, x>0.$ (iii)

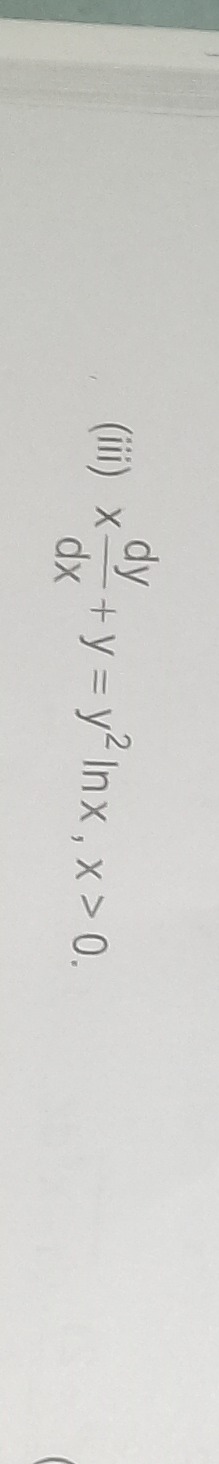
Answer 1

$y = \frac{2}{x(K - (\ln x)^2)}$

Answer 2

The given differential equation is a Bernoulli's equation. It is transformed into a first-order linear differential equation by substituting $v = y^{-1}$. The linear equation is then solved using an integrating factor. Finally, $v$ is replaced by $y^{-1}$ to obtain the general solution for $y$.

Answer: The general solution to the differential equation is $y = \frac{2}{x(K - (\ln x)^2)}$, where $K$ is an arbitrary constant.