Question
Question: $\frac{d}{dt}(\frac{at+b}{x})=?$...
dtd(xat+b)=?
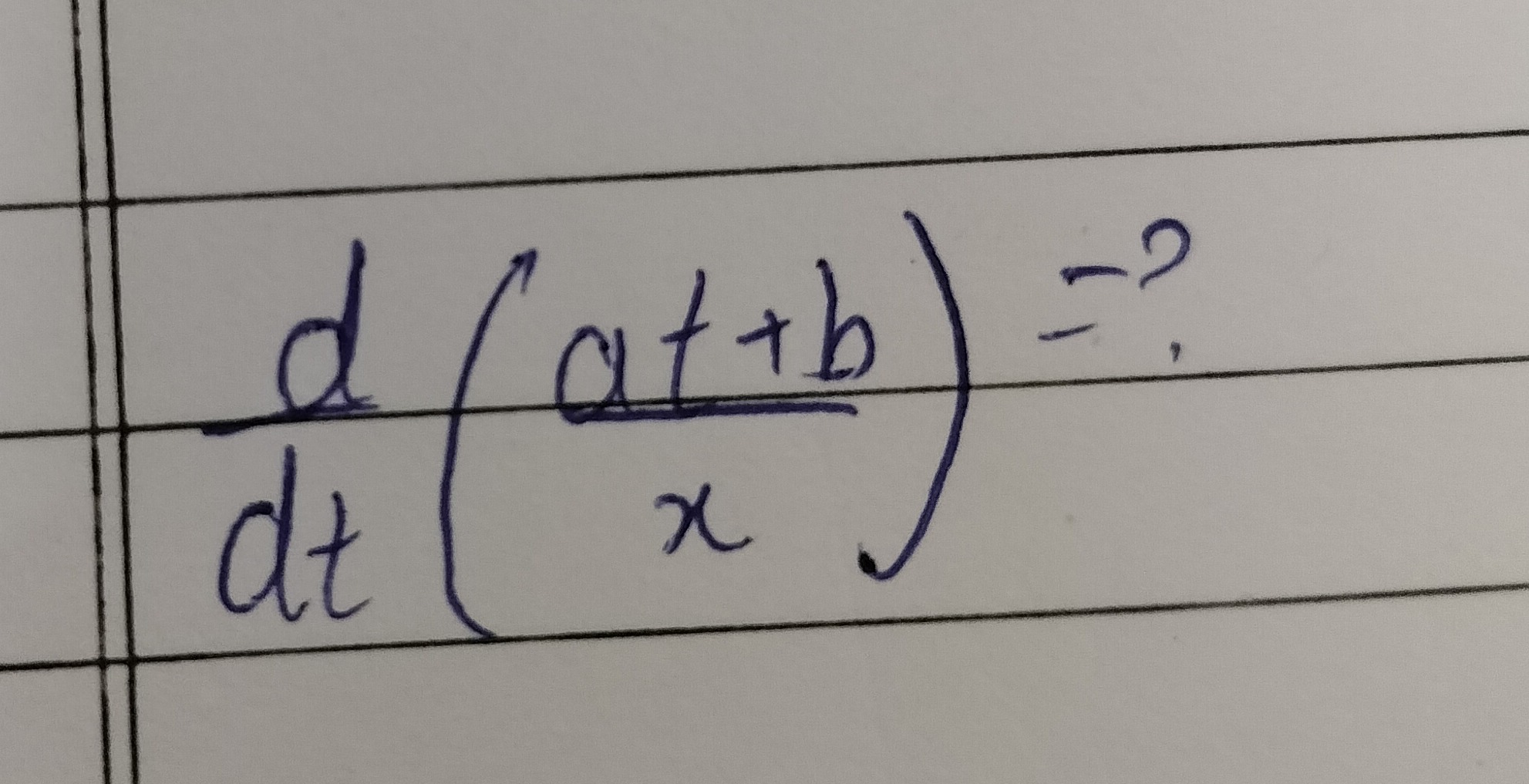
Answer
\frac{a}{x}
Explanation
Solution
The derivative is taken with respect to t. The expression is xat+b. Assume a,b, and x are constants with respect to t.
dtd(xat+b)=x1dtd(at+b)
dtd(at+b)=dtd(at)+dtd(b)=a⋅1+0=a
So, dtd(xat+b)=x1⋅a=xa.
