Question
Question: $\frac{cos6\theta + 6cos4\theta + 15cos2\theta + 10}{cos5\theta + 5cos3\theta + 10cos\theta} = \lamb...
cos5θ+5cos3θ+10cosθcos6θ+6cos4θ+15cos2θ+10=λcosθ
λ=?
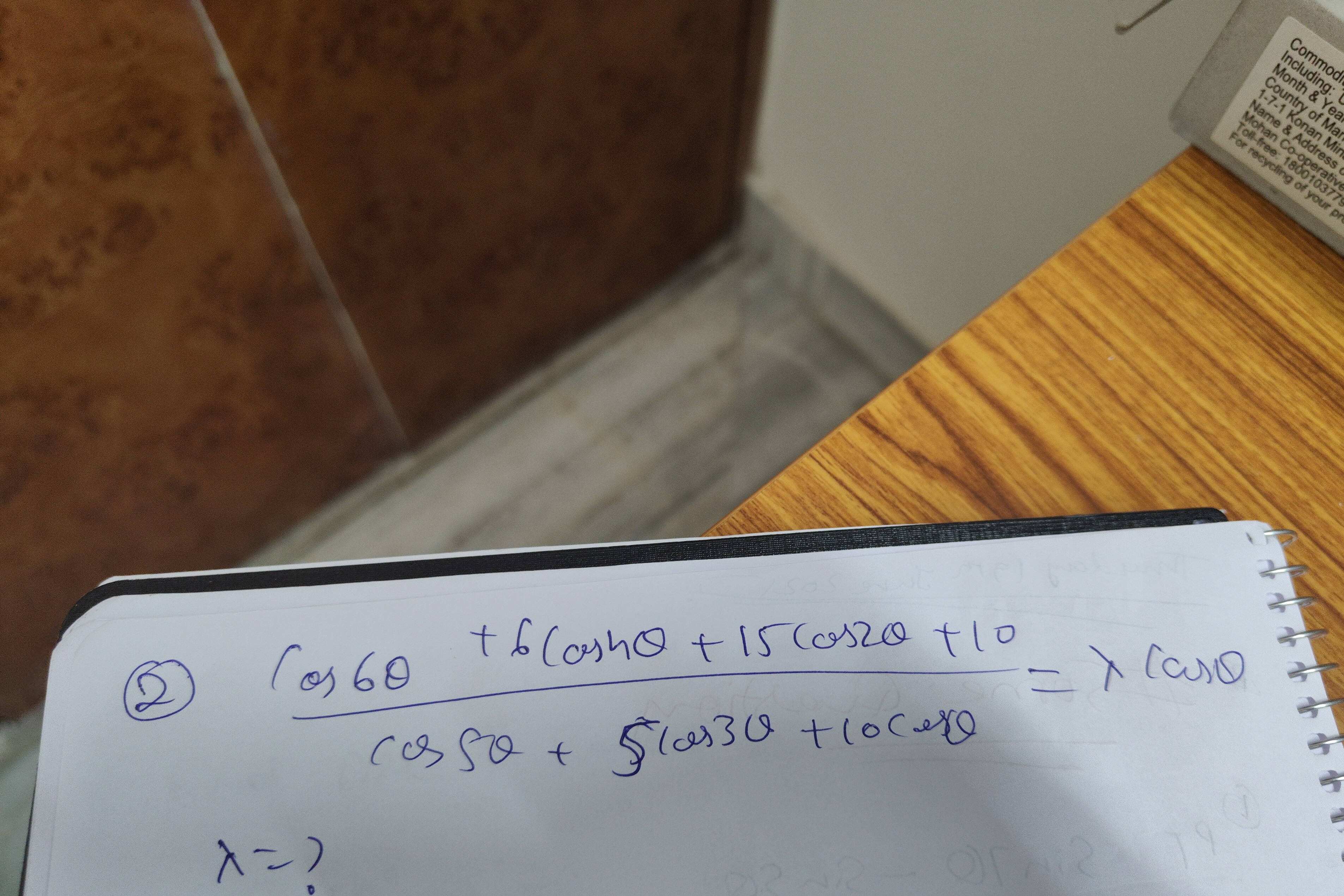
2
Solution
To solve the given problem, we need to simplify the expression on the left-hand side and compare it with λcosθ. The key to simplifying this expression lies in recognizing the numerator and denominator as expansions of powers of cosine in terms of multiple angles. These expansions are derived from De Moivre's theorem.
Let's recall the general formulas for expressing powers of cosθ in terms of multiple angles: Using 2cosθ=eiθ+e−iθ, we have (2cosθ)n=(eiθ+e−iθ)n. By binomial expansion and pairing terms, we get:
-
If n is an odd integer: 2n−1cosnθ=(0n)cosnθ+(1n)cos(n−2)θ+⋯+((n−1)/2n)cosθ This can be written as: 2n−1cosnθ=∑k=0(n−1)/2(kn)cos((n−2k)θ)
-
If n is an even integer: 2n−1cosnθ=(0n)cosnθ+(1n)cos(n−2)θ+⋯+(n/2−1n)cos2θ+21(n/2n) This can be written as: 2n−1cosnθ=∑k=0n/2−1(kn)cos((n−2k)θ)+21(n/2n)
Let's analyze the denominator: D=cos5θ+5cos3θ+10cosθ. Comparing this with the formula for odd n, we can see that for n=5: 25−1cos5θ=(05)cos(5θ)+(15)cos(5−2)θ+(25)cos(5−4)θ 16cos5θ=1cos5θ+5cos3θ+10cosθ Thus, the denominator D=16cos5θ.
Now, let's analyze the numerator: N=cos6θ+6cos4θ+15cos2θ+10. Comparing this with the formula for even n, we can see that for n=6: 26−1cos6θ=(06)cos(6θ)+(16)cos(6−2)θ+(26)cos(6−4)θ+21(6/26) 32cos6θ=1cos6θ+6cos4θ+15cos2θ+21(36) We know (36)=3×2×16×5×4=20. So, 32cos6θ=cos6θ+6cos4θ+15cos2θ+21(20) 32cos6θ=cos6θ+6cos4θ+15cos2θ+10 Thus, the numerator N=32cos6θ.
Now, substitute these simplified expressions for the numerator and denominator back into the original equation: DN=16cos5θ32cos6θ 16cos5θ32cos6θ=2cosθ We are given that cos5θ+5cos3θ+10cosθcos6θ+6cos4θ+15cos2θ+10=λcosθ. Comparing our result with the given equation: 2cosθ=λcosθ Assuming cosθ=0 (as the expression would be undefined otherwise), we can cancel cosθ from both sides: λ=2
