Question

$\frac{Br_2}{2} + OH^{\ominus} \longrightarrow Br^{\ominus} + BrO_3^{\ominus} + n_2O$ (Hot conc.)

red"

$n_{red}=2|-1-0|=2$

$n_{oxid^{n}}=2|5-0|=10$

Answer 1

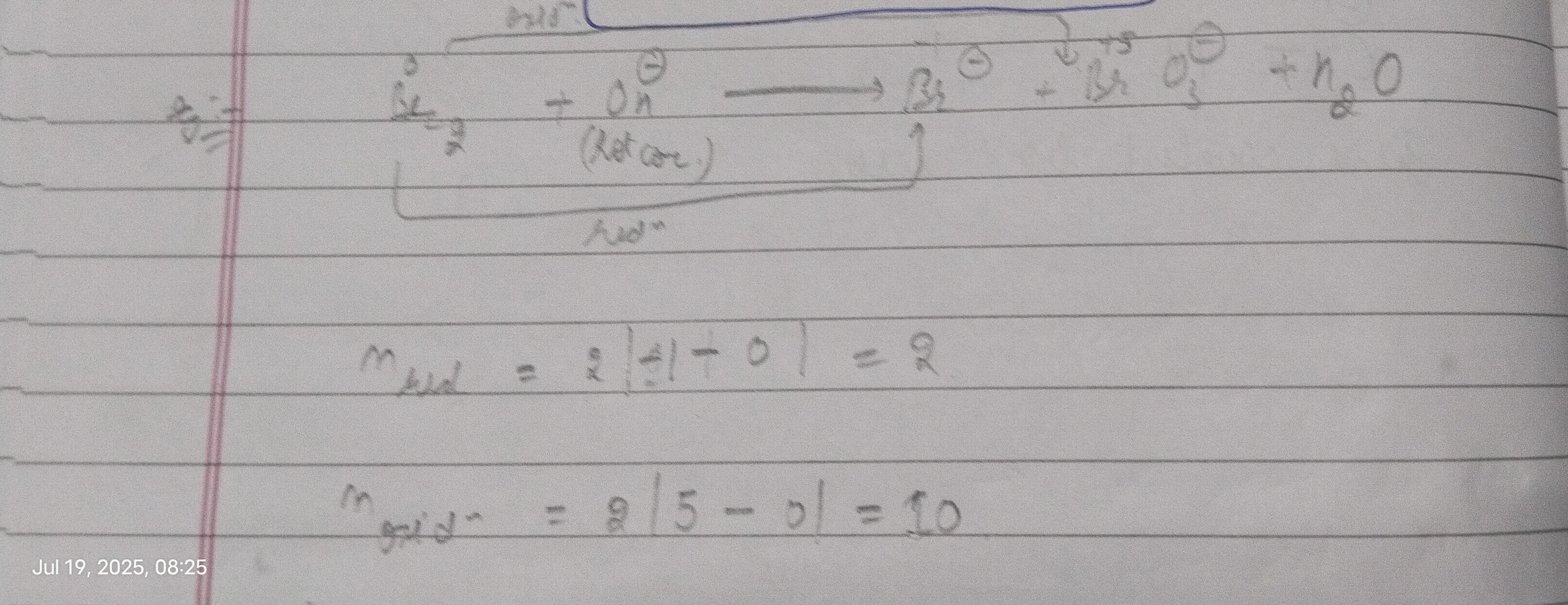
3Br_2 + 6OH^{\ominus} \longrightarrow 5Br^{\ominus} + BrO_3^{\ominus} + 3H_2O

Answer 2

The given reaction is a disproportionation reaction of Bromine in a hot concentrated hydroxide solution. Bromine (oxidation state 0) is simultaneously reduced to Bromide (oxidation state -1) and oxidized to Bromate (oxidation state +5).

The provided calculations are for the number of electrons transferred per $Br_2$ molecule in each half-reaction:

1. Reduction half-reaction: $Br_2 \longrightarrow Br^{\ominus}$

   • Oxidation state of Br changes from 0 to -1.
   • For one Br atom, the change is $|-1 - 0| = 1$.
   • Since $Br_2$ molecule contains 2 Br atoms, the total number of electrons gained ($n_{red}$) by one $Br_2$ molecule is $2 \times |-1 - 0| = 2 \times 1 = 2$.
   • This corresponds to the provided $n_{red}=2|-1-0|=2$.

2. Oxidation half-reaction: $Br_2 \longrightarrow BrO_3^{\ominus}$

   • Oxidation state of Br changes from 0 to +5.
   • For one Br atom, the change is $|+5 - 0| = 5$.
   • Since $Br_2$ molecule contains 2 Br atoms, the total number of electrons lost ($n_{oxid^n}$) by one $Br_2$ molecule is $2 \times |+5 - 0| = 2 \times 5 = 10$.
   • This corresponds to the provided $n_{oxid^{n}}=2|5-0|=10$.

These values are crucial for balancing the redox reaction using the oxidation state method or ion-electron method. The number of electrons gained must equal the number of electrons lost.

Balancing the reaction using the Ion-Electron Method (in basic medium):

Step 1: Write the unbalanced half-reactions. Reduction: $Br_2 \longrightarrow Br^{\ominus}$ Oxidation: $Br_2 \longrightarrow BrO_3^{\ominus}$

Step 2: Balance atoms other than O and H. Reduction: $Br_2 \longrightarrow 2Br^{\ominus}$ Oxidation: $Br_2 \longrightarrow 2BrO_3^{\ominus}$

Step 3: Balance O atoms by adding $H_2O$ and H atoms by adding $H^{\oplus}$. Then neutralize $H^{\oplus}$ with $OH^{\ominus}$ for basic medium.

• Reduction half-reaction: No O or H atoms. $Br_2 \longrightarrow 2Br^{\ominus}$
• Oxidation half-reaction: $Br_2 \longrightarrow 2BrO_3^{\ominus}$ (6 oxygen atoms on RHS) Balance O by adding $H_2O$: $Br_2 + 6H_2O \longrightarrow 2BrO_3^{\ominus}$ (12 H atoms on LHS) Balance H by adding $H^{\oplus}$: $Br_2 + 6H_2O \longrightarrow 2BrO_3^{\ominus} + 12H^{\oplus}$ Since the reaction is in basic medium, add $12OH^{\ominus}$ to both sides to neutralize $H^{\oplus}$: $Br_2 + 6H_2O + 12OH^{\ominus} \longrightarrow 2BrO_3^{\ominus} + 12H^{\oplus} + 12OH^{\ominus}$ Combine $H^{\oplus}$ and $OH^{\ominus}$ to form $H_2O$: $Br_2 + 6H_2O + 12OH^{\ominus} \longrightarrow 2BrO_3^{\ominus} + 12H_2O$ Cancel $H_2O$ molecules: $Br_2 + 12OH^{\ominus} \longrightarrow 2BrO_3^{\ominus} + 6H_2O$

Step 4: Balance charges by adding electrons.

• Reduction half-reaction: $Br_2 + 2e^{\ominus} \longrightarrow 2Br^{\ominus}$ (Charge: 0 on LHS, -2 on RHS. Add 2 electrons to LHS)
• Oxidation half-reaction: $Br_2 + 12OH^{\ominus} \longrightarrow 2BrO_3^{\ominus} + 6H_2O$ (Charge: -12 on LHS, -2 on RHS. Add 10 electrons to RHS) $Br_2 + 12OH^{\ominus} \longrightarrow 2BrO_3^{\ominus} + 6H_2O + 10e^{\ominus}$

Step 5: Make the number of electrons equal in both half-reactions. Multiply the reduction half-reaction by 5 and the oxidation half-reaction by 1 (to get 10 electrons on both sides). Reduction: $5(Br_2 + 2e^{\ominus} \longrightarrow 2Br^{\ominus}) \implies 5Br_2 + 10e^{\ominus} \longrightarrow 10Br^{\ominus}$ Oxidation: $1(Br_2 + 12OH^{\ominus} \longrightarrow 2BrO_3^{\ominus} + 6H_2O + 10e^{\ominus}) \implies Br_2 + 12OH^{\ominus} \longrightarrow 2BrO_3^{\ominus} + 6H_2O + 10e^{\ominus}$

Step 6: Add the balanced half-reactions and simplify. $5Br_2 + 10e^{\ominus} \longrightarrow 10Br^{\ominus}$ $Br_2 + 12OH^{\ominus} \longrightarrow 2BrO_3^{\ominus} + 6H_2O + 10e^{\ominus}$

$6Br_2 + 12OH^{\ominus} \longrightarrow 10Br^{\ominus} + 2BrO_3^{\ominus} + 6H_2O$

Divide all coefficients by 2 to get the simplest integer coefficients: $3Br_2 + 6OH^{\ominus} \longrightarrow 5Br^{\ominus} + BrO_3^{\ominus} + 3H_2O$

The balanced chemical equation is: $3Br_2 + 6OH^{\ominus} \longrightarrow 5Br^{\ominus} + BrO_3^{\ominus} + 3H_2O$

The provided values $n_{red}=2$ and $n_{oxid^n}=10$ are correctly calculated and represent the number of electrons transferred per $Br_2$ molecule in the reduction and oxidation pathways respectively.

The final answer is $\boxed{3Br_2 + 6OH^{\ominus} \longrightarrow 5Br^{\ominus} + BrO_3^{\ominus} + 3H_2O}$

Explanation of the solution: The given reaction is a disproportionation of $Br_2$ in basic medium. The oxidation state of Br changes from 0 to -1 (reduction) and from 0 to +5 (oxidation).

1. Calculate electrons transferred ($n$-factors for half-reactions):
   • For reduction ($Br_2 \to Br^-$): Each Br atom gains 1 electron. Since $Br_2$ has two Br atoms, $n_{red} = 2 \times 1 = 2$.
   • For oxidation ($Br_2 \to BrO_3^-$): Each Br atom loses 5 electrons. Since $Br_2$ has two Br atoms, $n_{oxid^n} = 2 \times 5 = 10$.
2. Balance electron transfer: To balance the electrons, the least common multiple of 2 and 10 is 10. This means 5 molecules of $Br_2$ are reduced (5 * 2 = 10 electrons gained) and 1 molecule of $Br_2$ is oxidized (1 * 10 = 10 electrons lost). Total $Br_2$ on reactant side will be $5+1=6$.
3. Balance half-reactions in basic medium:
   • Reduction: $Br_2 + 2e^{\ominus} \longrightarrow 2Br^{\ominus}$ (multiplied by 5)
   • Oxidation: $Br_2 + 12OH^{\ominus} \longrightarrow 2BrO_3^{\ominus} + 6H_2O + 10e^{\ominus}$ (multiplied by 1)
4. Combine and simplify: Add the balanced half-reactions and divide by the common factor (2) to get the simplest integer coefficients.

Answer: The balanced chemical equation is: $3Br_2 + 6OH^{\ominus} \longrightarrow 5Br^{\ominus} + BrO_3^{\ominus} + 3H_2O$

The provided $n_{red}=2|-1-0|=2$ and $n_{oxid^{n}}=2|5-0|=10$ correctly represent the number of electrons gained and lost per $Br_2$ molecule in the reduction and oxidation pathways, respectively.