Solveeit Logo
Login

Question

Question: If $\overrightarrow{V_1}, \overrightarrow{V_2}$ are two orthogonal unit vectors and $\overrightarrow...

If V1→,V2→\overrightarrow{V_1}, \overrightarrow{V_2} are two orthogonal unit vectors and V3→=V1→×V2→\overrightarrow{V_3}=\overrightarrow{V_1} \times \overrightarrow{V_2} then

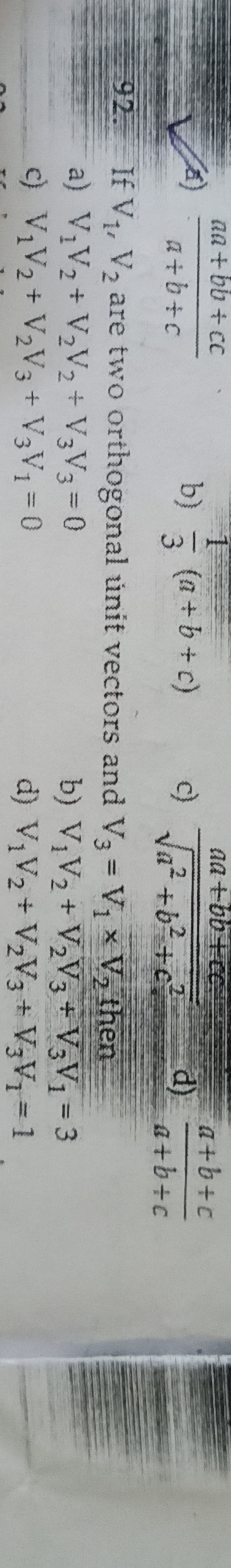
A

V1V2+V2V2+V3V3=0V_1V_2 + V_2V_2 + V_3V_3 = 0

B

V1V2+V2V3+V3V1=3V_1V_2 + V_2V_3 + V_3V_1 = 3

C

V1V2+V2V3+V3V1=0V_1V_2 + V_2V_3 + V_3V_1 = 0

D

V1V2+V2V3+V3V1=1V_1V_2 + V_2V_3 + V_3V_1 = 1

Answer

Option c) is correct.

Explanation

Solution

Given:

  • V1→\overrightarrow{V_1} and V2→\overrightarrow{V_2} are orthogonal unit vectors, so

    V1→⋅V1→=1,V2→⋅V2→=1,V1→⋅V2→=0.\overrightarrow{V_1} \cdot \overrightarrow{V_1} = 1,\quad \overrightarrow{V_2} \cdot \overrightarrow{V_2} = 1,\quad \overrightarrow{V_1} \cdot \overrightarrow{V_2} = 0.

  • V3→=V1→×V2→\overrightarrow{V_3} = \overrightarrow{V_1} \times \overrightarrow{V_2} is a unit vector orthogonal to both, hence

    V1→⋅V3→=0,V2→⋅V3→=0.\overrightarrow{V_1} \cdot \overrightarrow{V_3} = 0,\quad \overrightarrow{V_2} \cdot \overrightarrow{V_3} = 0.

Evaluating Option c):

Calculate

V1→⋅V2→+V2→⋅V3→+V3→⋅V1→=0+0+0=0.\overrightarrow{V_1} \cdot \overrightarrow{V_2} + \overrightarrow{V_2} \cdot \overrightarrow{V_3} + \overrightarrow{V_3} \cdot \overrightarrow{V_1} = 0 + 0 + 0 = 0.

Thus, Option c) is correct.

Core Explanation:

Since V1,V2V_1, V_2 are unit and orthogonal, their dot product is zero. The cross product V3=V1×V2V_3 = V_1 \times V_2 is orthogonal to both, giving all pairwise dot products in the expression V1⋅V2+V2⋅V3+V3⋅V1V_1 \cdot V_2 + V_2 \cdot V_3 + V_3 \cdot V_1 as zero; hence, the sum is 0.