Question
Question: $\frac{8}{\sqrt[3]{(2x^{2}-7x-5)^{11}}}$...
3(2x2−7x−5)118
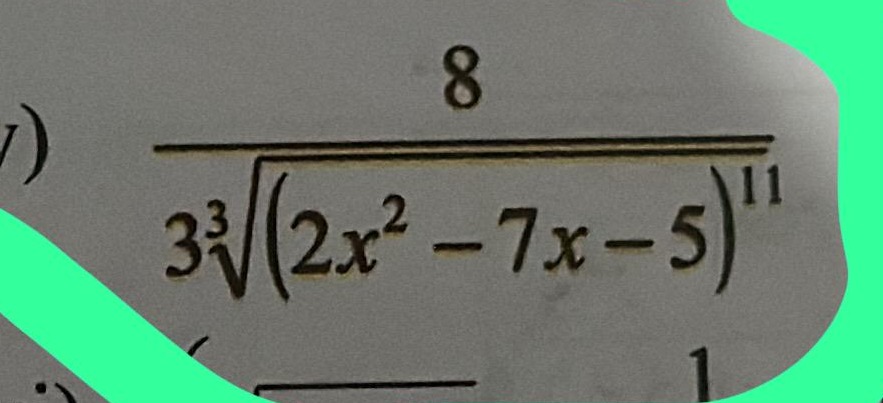
Answer
8(2x^{2}-7x-5)^{-11/3}
Explanation
Solution
The given expression is 3(2x2−7x−5)118.
Step 1: Convert the cube root into a fractional exponent.
We know that nA=A1/n. So, 3(2x2−7x−5)11=((2x2−7x−5)11)1/3.
Step 2: Apply the power of a power rule, (am)n=amn.
((2x2−7x−5)11)1/3=(2x2−7x−5)11×31=(2x2−7x−5)311.
Step 3: Rewrite the expression with the simplified denominator.
The expression becomes (2x2−7x−5)3118.
Step 4: Use the rule an1=a−n to move the term from the denominator to the numerator.
(2x2−7x−5)3118=8×(2x2−7x−5)−311.
The simplified expression is 8(2x2−7x−5)−11/3.
