Question

$\frac{6}{5}a^{\log_a x.\log_{10} a.\log_a 5} - 3^{\log_{10}(x/10)} = 9^{\log_{100} x+\log_4 2}$

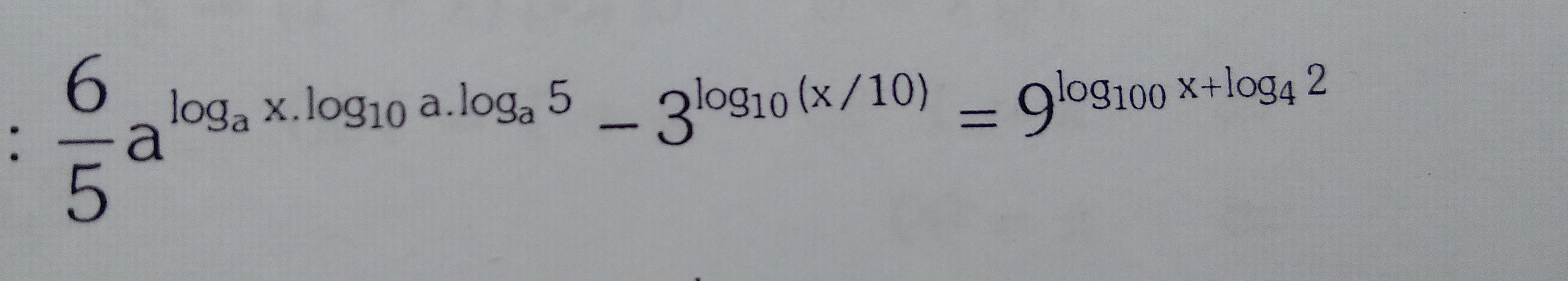
Answer 1

100

Answer 2

The equation was simplified by evaluating each term using logarithm properties. The first term $\frac{6}{5}a^{\log_a x.\log_{10} a.\log_a 5}$ simplifies to $\frac{6}{5} 5^{\log_{10} x}$, independent of $a$. The second term $- 3^{\log_{10}(x/10)}$ simplifies to $-\frac{1}{3} 3^{\log_{10} x}$. The third term $9^{\log_{100} x+\log_4 2}$ simplifies to $3 \cdot 3^{\log_{10} x}$. By setting $Y = \log_{10} x$, the equation transforms into $\frac{6}{5} 5^Y - \frac{1}{3} 3^Y = 3 \cdot 3^Y$. Rearranging and simplifying yields $(\frac{5}{3})^Y = \frac{25}{9}$, which implies $Y=2$. Substituting back $Y=\log_{10} x=2$, we get $x=10^2=100$.