Question
Question: $\frac{4}{8} = \frac{1}{2tan^2}$ $\forall \epsilon > 0.$...
84=2tan21
∀ϵ>0.
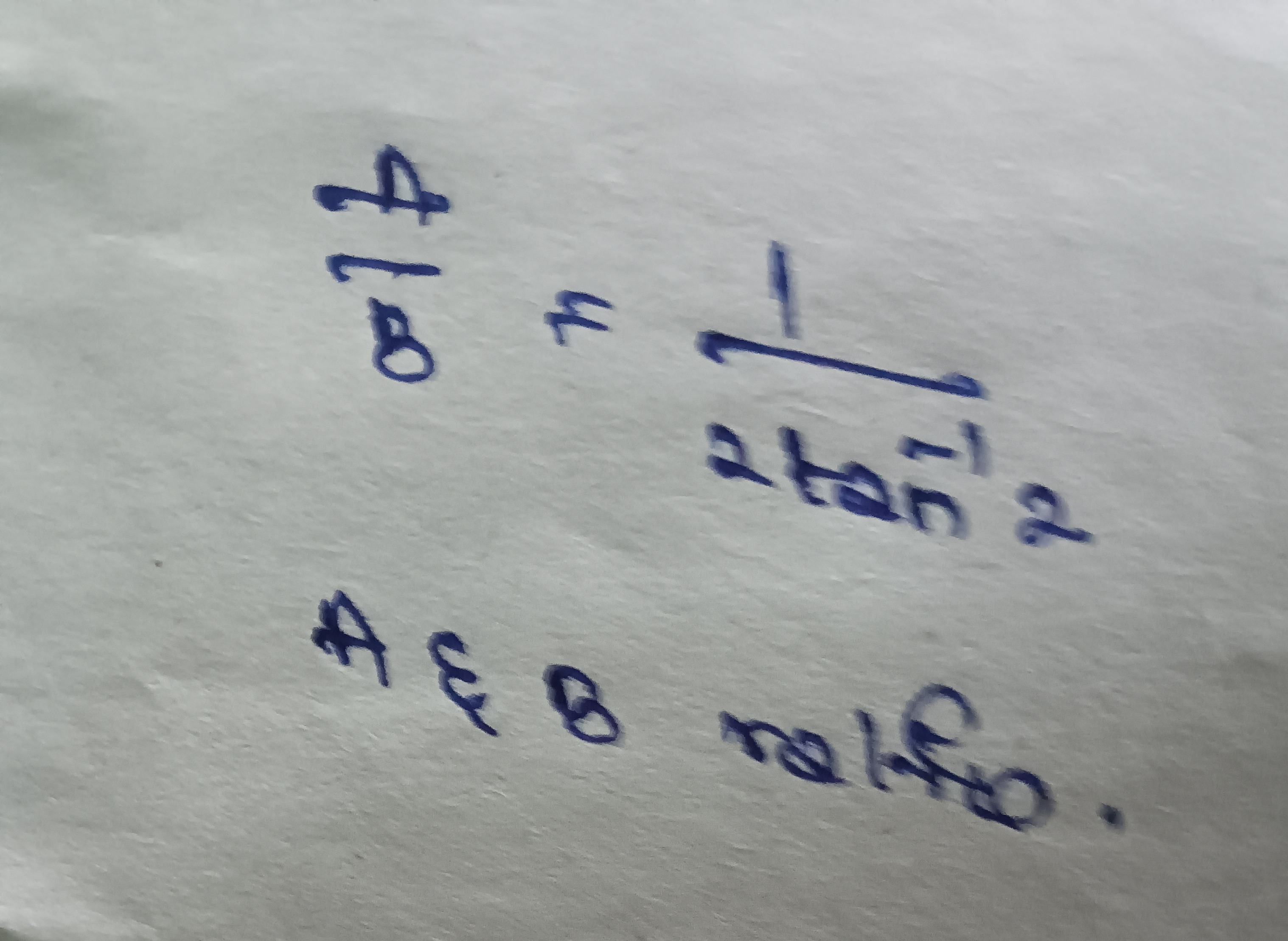
Answer
tan2=1
Explanation
Solution
The given equation is: 84=2tan21
Step 1: Simplify the left side of the equation. The fraction 84 can be simplified to 21. 21=2tan21
Step 2: Solve for tan2. To isolate tan2, we can take the reciprocal of both sides of the equation. 2=2tan2 Now, divide both sides by 2: 22=tan2 1=tan2 So, the value of tan2 is 1.
The condition ∀ϵ>0 is typically used in calculus for definitions of limits or continuity and is irrelevant to solving this algebraic trigonometric equation.
