Question
Question: $\frac{4}{8} = \frac{1}{2tan^{-1}2}$ A \& B ratio....
84=2tan−121
A & B ratio.
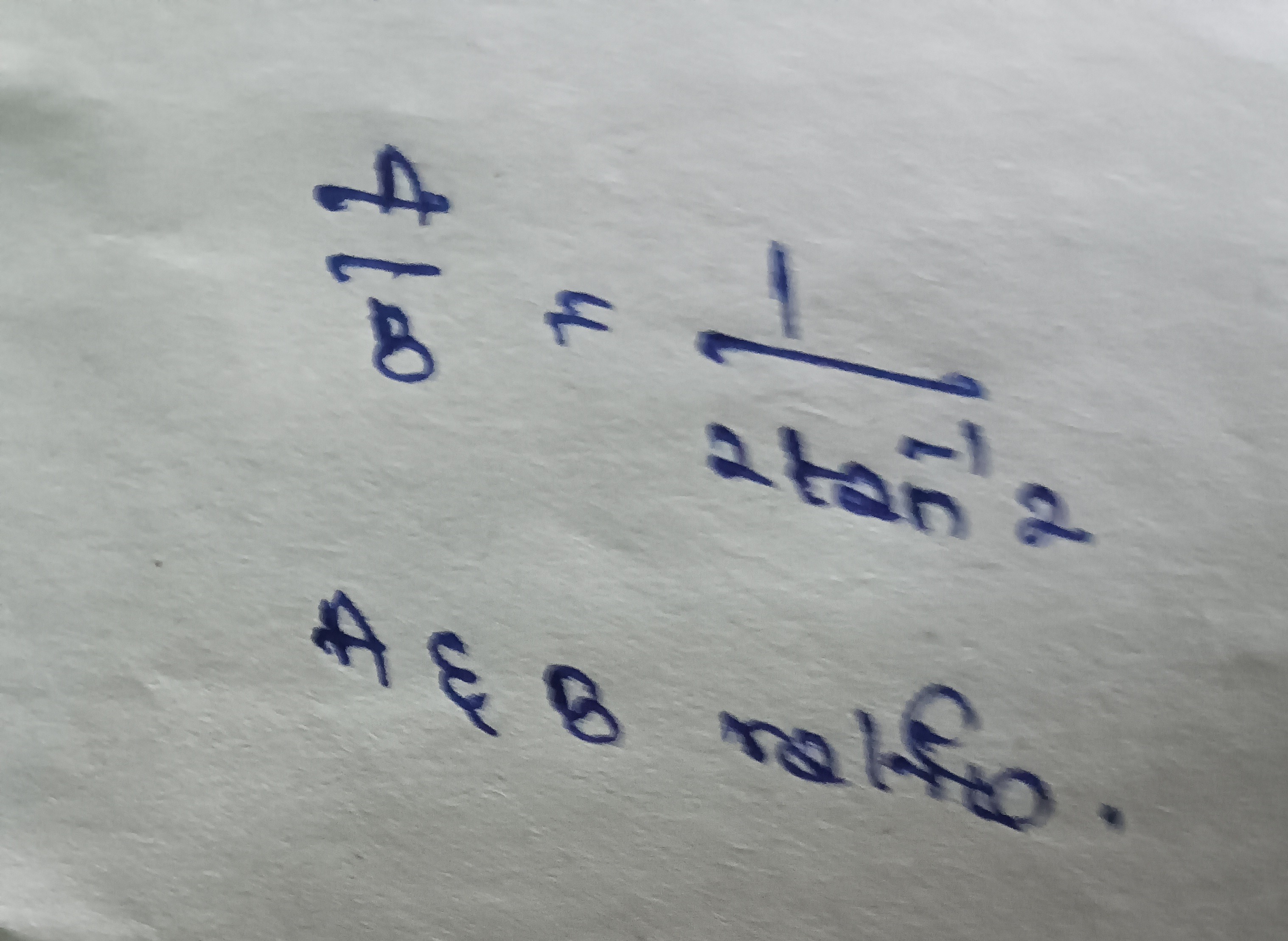
1:2
Solution
The given equation is: 84=2tan−121
A & B ratio.
First, let's analyze the given equation. The left side (LHS) is 84, which simplifies to 21. The right side (RHS) is 2tan−121. To check if the equality holds, we need to evaluate tan−12. Let x=tan−12. This means tanx=2. Using a calculator, tan−12≈1.107 radians. So, the RHS is 2×1.1071=2.2141≈0.4516. Since 0.5=0.4516, the given equation 84=2tan−121 is mathematically false.
The question then asks for "A & B ratio." There are no variables A or B explicitly defined in the equation. However, a common interpretation in such cases, especially when a fraction is presented, is to consider the numerator as 'A' and the denominator as 'B' from the most obvious part of the expression that forms a ratio.
From the fraction 84: Let A = 4 Let B = 8
The ratio of A to B is A:B, which is 4:8. This ratio can be simplified by dividing both numbers by their greatest common divisor, which is 4. 4÷4:8÷4=1:2.
The presence of the false equality involving tan−12 seems to be a distractor, or a test of critical thinking to identify irrelevant information, as the "A & B ratio" can be directly derived from the numbers 4 and 8.
The core solution is to identify A and B from the fraction 84 and calculate their ratio.
Explanation of the solution:
- Identify A and B from the fraction 84: A=4, B=8.
- Calculate the ratio A:B: 4:8.
- Simplify the ratio: 1:2.
- The truth value of the given equation is irrelevant to finding the ratio of A and B when they are interpreted as the numerator and denominator of the fraction 84.
