Question

$\frac{2}{3}\int_{0}^{100}e^{\{x\}}dx$

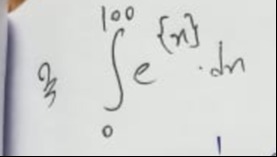
Answer 1

$\frac{200}{3}(e-1)$

Answer 2

The function $e^{\{x\}}$ is periodic with period 1. The integral of a periodic function $f(x)$ with period $T$ over an interval of length $nT$ is $n$ times the integral over one period: $\int_{0}^{nT} f(x) dx = n \int_{0}^{T} f(x) dx$. For $x \in [0, 1)$, $\{x\} = x$. Thus, $\int_{0}^{1} e^{\{x\}} dx = \int_{0}^{1} e^x dx = e-1$. Therefore, $\int_{0}^{100} e^{\{x\}} dx = 100(e-1)$. The required value is $\frac{2}{3} \times 100(e-1) = \frac{200}{3}(e-1)$.