Question
Question: $\frac{1}{x^3(1+x)^{3/2}}.$...
x3(1+x)3/21.
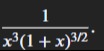
4x21+x15x2+5x−2+815ln1+x+11+x−1+C
Solution
To evaluate the integral I=∫x3(1+x)3/21dx, we use the substitution method.
The integrand is of the form ∫xm(a+bxn)pdx. Here, m=−3, a=1, b=1, n=1, and p=−3/2. Since nm+1=1−3+1=−2, which is an integer, the appropriate substitution is a+bxn=tk, where k is the denominator of p. So, we let 1+x=t2.
From 1+x=t2:
- x=t2−1
- dx=2tdt
- (1+x)3/2=(t2)3/2=t3
- x3=(t2−1)3
Substitute these into the integral: I=∫(t2−1)3⋅t31⋅(2tdt) I=∫t3(t2−1)32tdt I=∫t2(t2−1)32dt
Now, we use partial fraction decomposition for the integrand t2(t2−1)32. Let y=t2. Then the expression becomes y(y−1)32. We decompose this into partial fractions: y(y−1)32=yA+y−1B+(y−1)2C+(y−1)3D To find the coefficients A, B, C, D: Multiply both sides by y(y−1)3: 2=A(y−1)3+By(y−1)2+Cy(y−1)+Dy
Set y=1: 2=D(1)⟹D=2. Set y=0: 2=A(−1)3⟹A=−2.
Now, substitute A=−2 and D=2 back into the equation: 2=−2(y−1)3+By(y−1)2+Cy(y−1)+2y 2=−2(y3−3y2+3y−1)+B(y3−2y2+y)+C(y2−y)+2y 2=−2y3+6y2−6y+2+By3−2By2+By+Cy2−Cy+2y
Equating coefficients of powers of y: Coefficient of y3: 0=−2+B⟹B=2. Coefficient of y2: 0=6−2B+C⟹0=6−2(2)+C⟹0=2+C⟹C=−2.
So, the partial fraction decomposition is: y(y−1)32=−y2+y−12−(y−1)22+(y−1)32
Substitute back y=t2: I=∫(−t22+t2−12−(t2−1)22+(t2−1)32)dt
Now, integrate each term:
-
∫−t22dt=−2∫t−2dt=−2(−1t−1)=t2
-
∫t2−12dt=2∫(t−1)(t+1)1dt=2∫21(t−11−t+11)dt =∫(t−11−t+11)dt=ln∣t−1∣−ln∣t+1∣=lnt+1t−1
-
∫−(t2−1)22dt=−2∫(t2−1)21dt Use the reduction formula ∫(x2−a2)n1dx=2a2(n−1)(x2−a2)n−1−x−2a2(n−1)2n−3∫(x2−a2)n−11dx. For n=2,a=1: ∫(t2−1)21dt=2(1)(1)(t2−1)1−t−2(1)(1)2(2)−3∫(t2−1)11dt =2(t2−1)−t−21∫(t−1)(t+1)1dt =2(t2−1)−t−21⋅21lnt+1t−1=2(t2−1)−t−41lnt+1t−1. So, −2∫(t2−1)21dt=−2(2(t2−1)−t−41lnt+1t−1)=t2−1t+21lnt+1t−1.
-
∫(t2−1)32dt=2∫(t2−1)31dt Using the reduction formula for n=3,a=1: ∫(t2−1)31dt=2(1)(2)(t2−1)2−t−2(1)(2)2(3)−3∫(t2−1)21dt =4(t2−1)2−t−43∫(t2−1)21dt Substitute the result from step 3 for ∫(t2−1)21dt: =4(t2−1)2−t−43(2(t2−1)−t−41lnt+1t−1) =4(t2−1)2−t+8(t2−1)3t+163lnt+1t−1. So, 2∫(t2−1)31dt=2(4(t2−1)2−t+8(t2−1)3t+163lnt+1t−1) =2(t2−1)2−t+4(t2−1)3t+83lnt+1t−1.
Now, sum all the integrated terms: I=t2+lnt+1t−1+(t2−1t+21lnt+1t−1)+(2(t2−1)2−t+4(t2−1)3t+83lnt+1t−1)+C
Combine logarithmic terms: (1+21+83)lnt+1t−1=(88+4+3)lnt+1t−1=815lnt+1t−1.
Combine terms with t2−1t: (1+43)t2−1t=47t2−1t.
So, the integral is: I=t2+4(t2−1)7t−2(t2−1)2t+815lnt+1t−1+C
Substitute back t=1+x and t2−1=x: I=1+x2+4x71+x−2x21+x+815ln1+x+11+x−1+C
Combine the algebraic terms: 1+x2+4x71+x−2x21+x Find a common denominator, which is 4x21+x: =4x21+x2⋅4x2+4x21+x71+x⋅x1+x−4x21+x1+x⋅21+x =4x21+x8x2+7x(1+x)−2(1+x) =4x21+x8x2+7x+7x2−2−2x =4x21+x15x2+5x−2
Thus, the final integral is: I=4x21+x15x2+5x−2+815ln1+x+11+x−1+C
