Question
Question: $\frac{1+x}{1-x} \theta \leftarrow x$...
1−x1+xθ←x
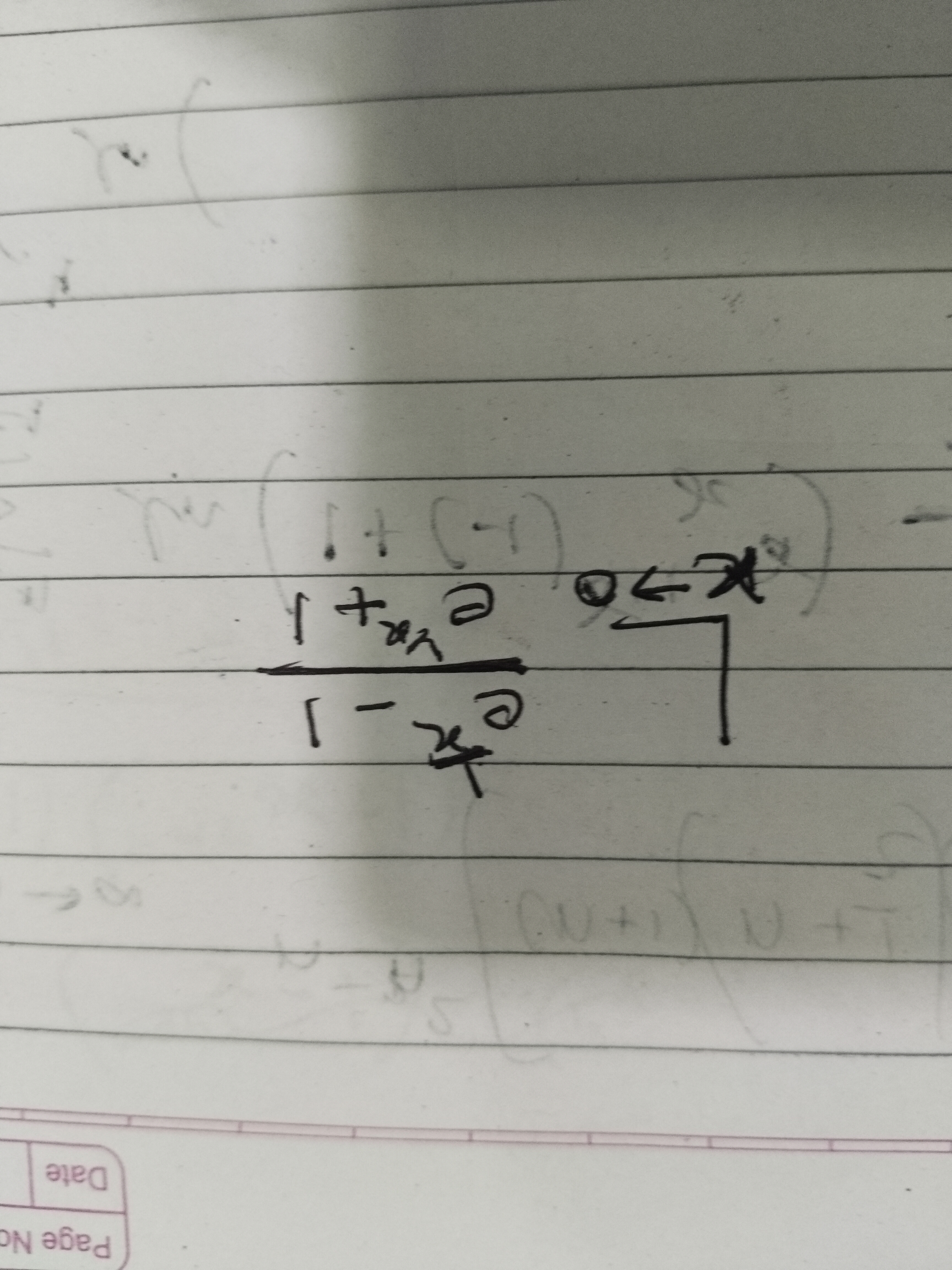
tan(4π+θ)
Solution
The provided input "1−x1+xθ←x" is ambiguous due to the non-standard notation "θ←x". However, in the context of JEE/NEET exams, the expression 1−x1+x frequently appears in problems involving trigonometric substitutions, particularly when dealing with inverse trigonometric functions or complex numbers.
The most common and relevant interpretation for this type of problem is to assume that the notation implies a relationship between x and θ, specifically a substitution that simplifies the expression. The standard substitution for the form 1−x1+x is x=tanθ.
Solution:
Let's assume the implied task is to simplify the expression 1−x1+x by substituting x=tanθ.
-
Substitute x=tanθ into the expression: 1−x1+x=1−tanθ1+tanθ
-
Recognize the trigonometric identity:
The expression 1−tanθ1+tanθ is a standard trigonometric identity derived from the tangent addition formula, tan(A+B)=1−tanAtanBtanA+tanB. We know that tan(4π)=1. So, we can rewrite the expression as: 1−tanθ1+tanθ=1−tan(4π)tanθtan(4π)+tanθ
-
Apply the tangent addition formula: 1−tan(4π)tanθtan(4π)+tanθ=tan(4π+θ)
Therefore, under the substitution x=tanθ, the expression 1−x1+x simplifies to tan(4π+θ).
Explanation of the solution:
The expression 1−x1+x is a common form in trigonometry. By substituting x=tanθ, it transforms into 1−tanθ1+tanθ. This is a direct application of the tangent addition formula tan(A+B)=1−tanAtanBtanA+tanB, with A=4π (since tan(4π)=1) and B=θ. Thus, the expression simplifies to tan(4π+θ).
