Question
Question: \[\frac{1}{4}\sum_{k=3}^{n}\frac{(k-1)^{2}(k-2)^{2}}{k^{2}}\]...
41∑k=3nk2(k−1)2(k−2)2
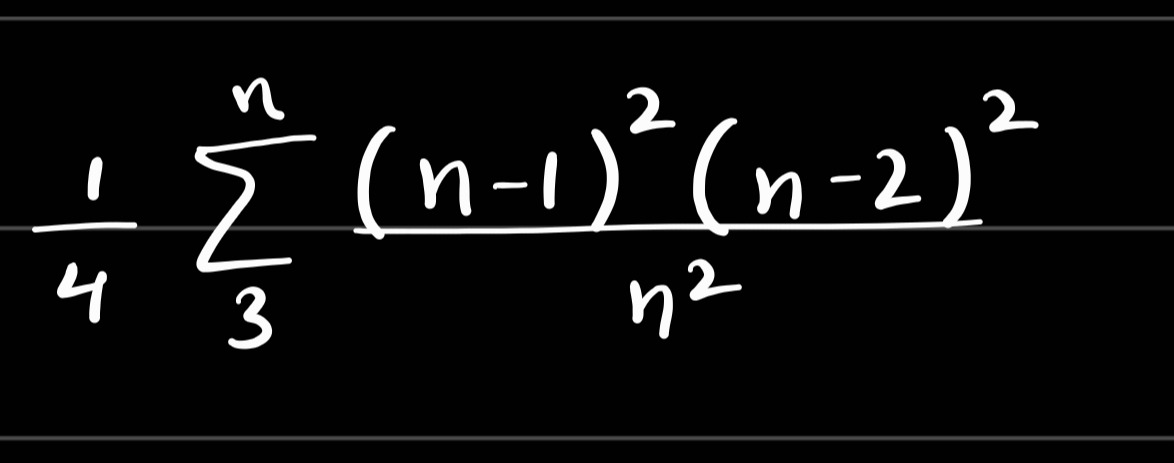
Answer
41[6n(n+1)(2n+1)−5−6(2n(n+1)−3)+13(n−2)−12(Hn−23)+4k=3∑nk21]
Explanation
Solution
Step 1. Simplify the general term:
k2(k−1)2(k−2)2=(k(k−1)(k−2))2=(k−3+k2)2=k2−6k+13−k12+k24.Step 2. Split the sum:
k=3∑n(k2−6k+13−k12+k24)=∑k2−6∑k+13∑1−12∑k1+4∑k21.Step 3. Use standard results:
- ∑k=3nk2=6n(n+1)(2n+1)−5
- ∑k=3nk=2n(n+1)−3
- ∑k=3n1=n−2
- ∑k=3nk1=Hn−1−21=Hn−23
- ∑k=3nk21 remains as is or can be written =ζ(2)−1−41−∑k>n1/k2.
Step 4. Multiply the total by 41 to obtain the final closed‑form:
41[6n(n+1)(2n+1)−5−6(2n(n+1)−3)+13(n−2)−12(Hn−23)+4k=3∑nk21].