Question

$\frac{1}{2\pi KL}$[lnx]$_a^b$=$\frac{1}{2\pi KL}$

ARJUNA

A cylindrical brass boiler of radius 15cm and thickness 1.0cm is filled with water and placed in electric heater. If water boils at rate of 200gm/sec. estimate temp of filament (L$_v$= 2.2 x 10$^6$, K=109J/s-m°C

Answer 1

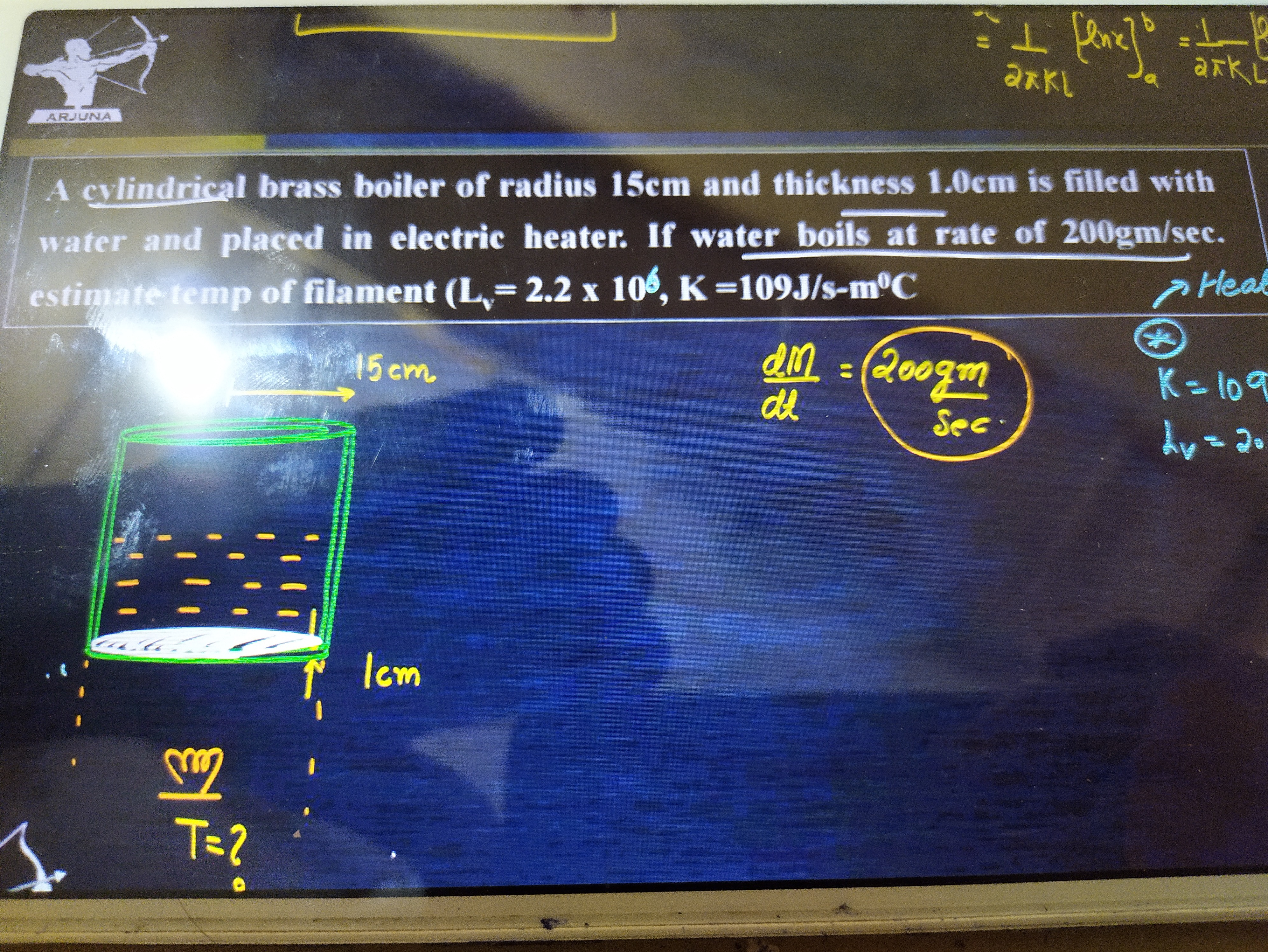
671.07°C

Answer 2

The problem describes a cylindrical brass boiler with a given radius and thickness, which is used to boil water at a specified rate. We need to estimate the temperature of the electric heater's filament.

1. Identify Given Parameters:

• Radius of the boiler, $r = 15 \text{ cm} = 0.15 \text{ m}$
• Thickness of the boiler's base (through which heat is conducted), $L = 1.0 \text{ cm} = 0.01 \text{ m}$
• Rate of water boiling, $\frac{dM}{dt} = 200 \text{ gm/sec} = 0.2 \text{ kg/sec}$
• Latent heat of vaporization of water, $L_v = 2.2 \times 10^6 \text{ J/kg}$
• Thermal conductivity of brass, $K = 109 \text{ J/s-m}^\circ\text{C}$
• Boiling temperature of water (at atmospheric pressure), $T_{water} = 100^\circ\text{C}$

2. Calculate the Area of Heat Transfer: Heat is transferred through the circular base of the cylindrical boiler. Area, $A = \pi r^2 = \pi (0.15 \text{ m})^2 = 0.0225\pi \text{ m}^2$

3. Calculate the Rate of Heat Required to Boil Water: The rate at which heat is absorbed by the water to vaporize is given by: $\frac{dQ}{dt} = \frac{dM}{dt} \times L_v$ $\frac{dQ}{dt} = 0.2 \text{ kg/s} \times 2.2 \times 10^6 \text{ J/kg} = 0.44 \times 10^6 \text{ J/s} = 440000 \text{ W}$

4. Apply Fourier's Law of Heat Conduction: The rate of heat transfer by conduction through the boiler's base is given by: $\frac{dQ}{dt} = \frac{K A \Delta T}{L}$ Where $\Delta T = T_{filament} - T_{water}$ is the temperature difference across the thickness of the boiler.

5. Solve for the Filament Temperature ($T_{filament}$): Equating the heat required for boiling to the heat transferred by conduction: $440000 \text{ W} = \frac{109 \text{ J/s-m}^\circ\text{C} \times (0.0225\pi \text{ m}^2) \times (T_{filament} - 100^\circ\text{C})}{0.01 \text{ m}}$

Rearranging the equation to solve for $T_{filament}$: $440000 \times 0.01 = 109 \times 0.0225\pi \times (T_{filament} - 100)$ $4400 = (109 \times 0.0225 \times \pi) \times (T_{filament} - 100)$ $4400 = (2.4525 \times \pi) \times (T_{filament} - 100)$ Using $\pi \approx 3.14159$: $4400 \approx (2.4525 \times 3.14159) \times (T_{filament} - 100)$ $4400 \approx 7.704665 \times (T_{filament} - 100)$

$T_{filament} - 100 \approx \frac{4400}{7.704665}$ $T_{filament} - 100 \approx 571.07^\circ\text{C}$ $T_{filament} \approx 571.07^\circ\text{C} + 100^\circ\text{C}$ $T_{filament} \approx 671.07^\circ\text{C}$

The temperature of the filament is approximately $671^\circ\text{C}$.

Explanation of the solution:

1. Calculate the heat transfer area ($A = \pi r^2$).
2. Determine the rate of heat required to vaporize water ($\frac{dQ}{dt} = \frac{dM}{dt} \times L_v$).
3. Apply Fourier's Law of heat conduction through the boiler's base ($\frac{dQ}{dt} = \frac{K A (T_{filament} - T_{water})}{L}$).
4. Substitute known values and solve for $T_{filament}$, assuming water boils at $100^\circ\text{C}$.

Answer:

The estimated temperature of the filament is approximately $671.07^\circ\text{C}$.