Solveeit Logo
Login

Question

Question: $\frac{(1^2 + 2^2 + 3^2 \dots n^2)!}{(1!)^2 \cdot (2!)^3 \cdot (3!)^4 \dots (n!)^{n+1}}$...

(12+22+32…n2)!(1!)2⋅(2!)3⋅(3!)4…(n!)n+1\frac{(1^2 + 2^2 + 3^2 \dots n^2)!}{(1!)^2 \cdot (2!)^3 \cdot (3!)^4 \dots (n!)^{n+1}}

Answer

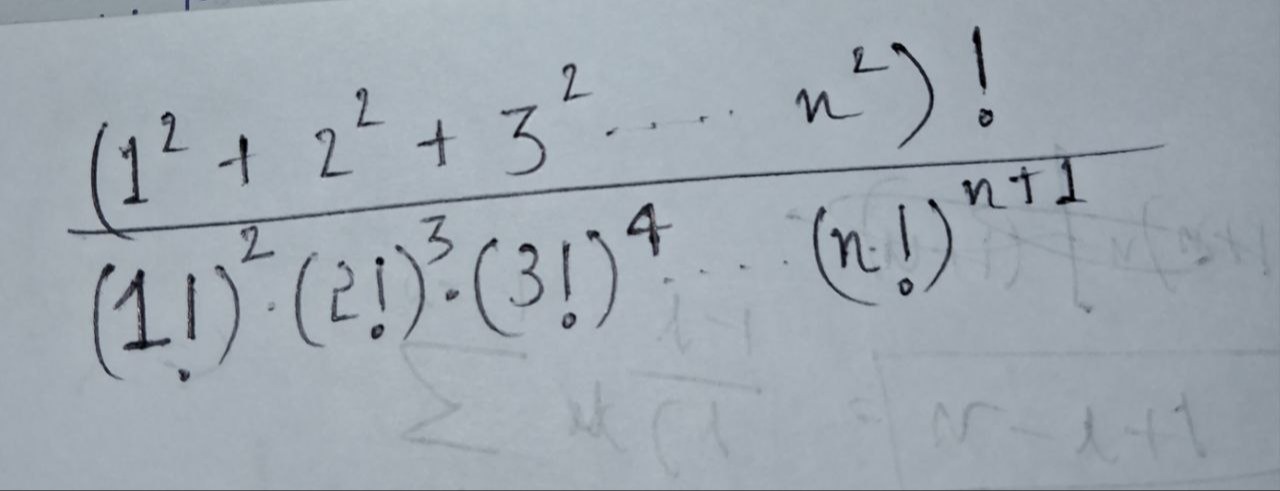
The expression is:

(n(n+1)(2n+1)6)!∏k=1n(k!)k+1\frac{\left( \frac{n(n+1)(2n+1)}{6} \right)!}{\prod_{k=1}^{n} (k!)^{k+1}}

This is the most simplified form of the given expression.

Explanation

Solution

The given expression is: (12+22+32+⋯+n2)!(1!)2⋅(2!)3⋅(3!)4⋅⋯⋅(n!)n+1\frac{(1^2 + 2^2 + 3^2 + \dots + n^2)!}{(1!)^2 \cdot (2!)^3 \cdot (3!)^4 \cdot \dots \cdot (n!)^{n+1}}

Let's analyze the numerator and the denominator separately.

Numerator: The sum of the first nn squares is given by the formula: ∑k=1nk2=n(n+1)(2n+1)6\sum_{k=1}^{n} k^2 = \frac{n(n+1)(2n+1)}{6} So, the numerator is (n(n+1)(2n+1)6)!\left( \frac{n(n+1)(2n+1)}{6} \right)!.

Denominator: The denominator is a product of powers of factorials: (1!)2⋅(2!)3⋅(3!)4⋅⋯⋅(n!)n+1=∏k=1n(k!)k+1(1!)^2 \cdot (2!)^3 \cdot (3!)^4 \cdot \dots \cdot (n!)^{n+1} = \prod_{k=1}^{n} (k!)^{k+1}

Let's evaluate the expression for small values of nn to see if a pattern emerges.

Case n = 1: Numerator: (12)!=1!=1(1^2)! = 1! = 1 Denominator: (1!)1+1=(1!)2=12=1(1!)^{1+1} = (1!)^2 = 1^2 = 1 Value of expression = 11=1\frac{1}{1} = 1.

Case n = 2: Numerator: (12+22)!=(1+4)!=5!=120(1^2 + 2^2)! = (1 + 4)! = 5! = 120 Denominator: (1!)2⋅(2!)3=(1)2⋅(2)3=1⋅8=8(1!)^2 \cdot (2!)^3 = (1)^2 \cdot (2)^3 = 1 \cdot 8 = 8 Value of expression = 1208=15\frac{120}{8} = 15.

Case n = 3: Numerator: (12+22+32)!=(1+4+9)!=14!=87,178,291,200(1^2 + 2^2 + 3^2)! = (1 + 4 + 9)! = 14! = 87,178,291,200 Denominator: (1!)2⋅(2!)3⋅(3!)4=(1)2⋅(2)3⋅(6)4=1⋅8⋅1296=10368(1!)^2 \cdot (2!)^3 \cdot (3!)^4 = (1)^2 \cdot (2)^3 \cdot (6)^4 = 1 \cdot 8 \cdot 1296 = 10368 Value of expression = 14!10368=87,178,291,20010368=8,408,400\frac{14!}{10368} = \frac{87,178,291,200}{10368} = 8,408,400.

The sequence of values is 1,15,8408400,…1, 15, 8408400, \dots. This sequence does not appear to simplify to a common elementary function or a simple closed-form expression in terms of nn. The expression is already in its most simplified general form as a ratio of factorials. Without a specific value for nn, or further context (e.g., if it's part of a larger identity or a specific type of combinatorial problem), it cannot be "solved" into a more compact or simpler algebraic expression.

Therefore, the expression itself is the most "solved" form possible in general terms.

The question asks to "solve" the expression. If it implies finding a simplified closed form, such a form is not generally available for this type of complex factorial ratio. The expression as written is the most accurate representation.

The problem likely expects the recognition that the numerator is the factorial of the sum of squares and the denominator is a product of powers of factorials.