Question
Question: $\frac{1-\sqrt{1-4x^2}}{x}<3$...
x1−1−4x2<3
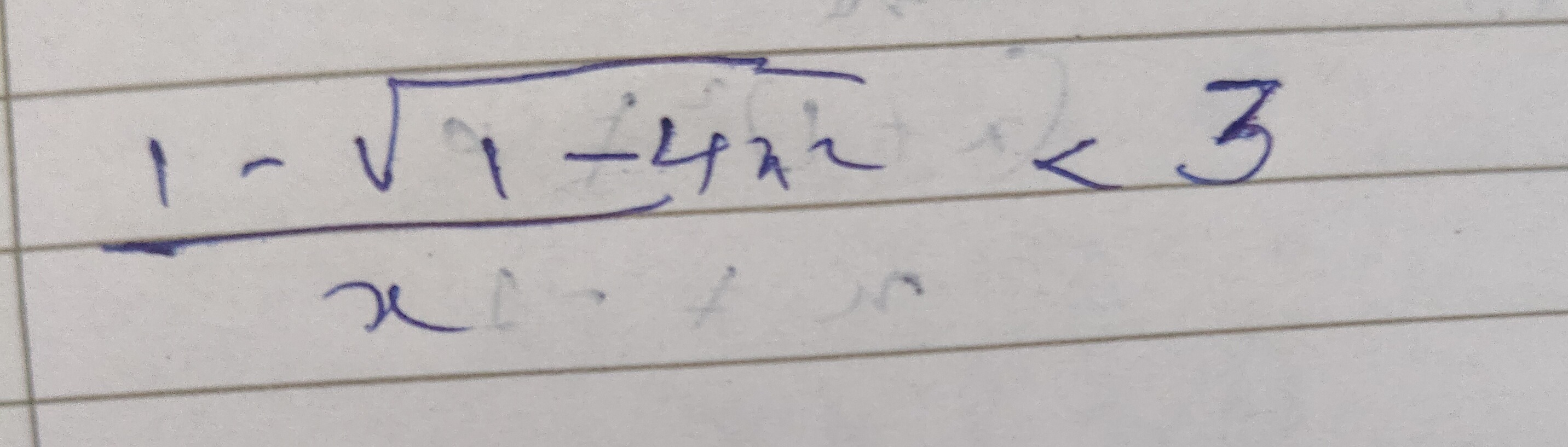
[−21,0)∪(0,21]
Solution
To solve the inequality x1−1−4x2<3, we first determine the domain of the expression.
-
Domain of the expression:
For 1−4x2 to be defined, we must have 1−4x2≥0.
1≥4x2⟹x2≤41⟹−21≤x≤21.
Also, the denominator x cannot be zero, so x=0.
Combining these, the domain for x is x∈[−21,0)∪(0,21]. -
Solve the inequality by considering cases based on the sign of x:
Case 1: x>0
In this case, x∈(0,21]. Multiply both sides of the inequality by x (which is positive), so the inequality sign remains the same:
1−1−4x2<3x
1−3x<1−4x2We need to consider two sub-cases for 1−3x:
-
Subcase 1.1: 1−3x<0
This implies 3x>1, so x>31.
For these values, x∈(31,21] (intersecting with the domain x∈(0,21]).
If 1−3x is negative, then 1−3x<1−4x2 is always true, because 1−4x2 is always non-negative.
So, x∈(31,21] is part of the solution. -
Subcase 1.2: 1−3x≥0
This implies 3x≤1, so x≤31.
For these values, x∈(0,31] (intersecting with the domain x∈(0,21]).
Since both sides of 1−3x<1−4x2 are non-negative, we can square both sides:
(1−3x)2<(1−4x2)2
1−6x+9x2<1−4x2
13x2−6x<0
x(13x−6)<0
This inequality holds when 0<x<136.
Intersecting this with x∈(0,31]: Since 31=3913 and 136=3918, we have 31<136.
So, the intersection is x∈(0,31].
Combining the solutions from Subcase 1.1 and Subcase 1.2 for x>0:
(31,21]∪(0,31]=(0,21].Case 2: x<0
In this case, x∈[−21,0). Multiply both sides of the inequality by x (which is negative), so the inequality sign reverses:
1−1−4x2>3x
1−3x>1−4x2
Since x<0, 1−3x will be positive (e.g., if x=−0.1, 1−3(−0.1)=1.3). The right side 1−4x2 is non-negative. Since both sides are non-negative (LHS is positive, RHS is non-negative), we can square both sides:
(1−3x)2>(1−4x2)2
1−6x+9x2>1−4x2
13x2−6x>0
x(13x−6)>0
This inequality holds when x<0 or x>136.
Intersecting this with the domain for this case, x∈[−21,0):
The part x>136 does not intersect with x∈[−21,0).
The part x<0 intersects with x∈[−21,0) to give x∈[−21,0). -
-
Combine the solutions from Case 1 and Case 2:
The solution for x>0 is x∈(0,21].
The solution for x<0 is x∈[−21,0).
The overall solution is the union of these two sets:
x∈[−21,0)∪(0,21].
The solution covers all values within the domain of the expression, except for x=0.
