Question
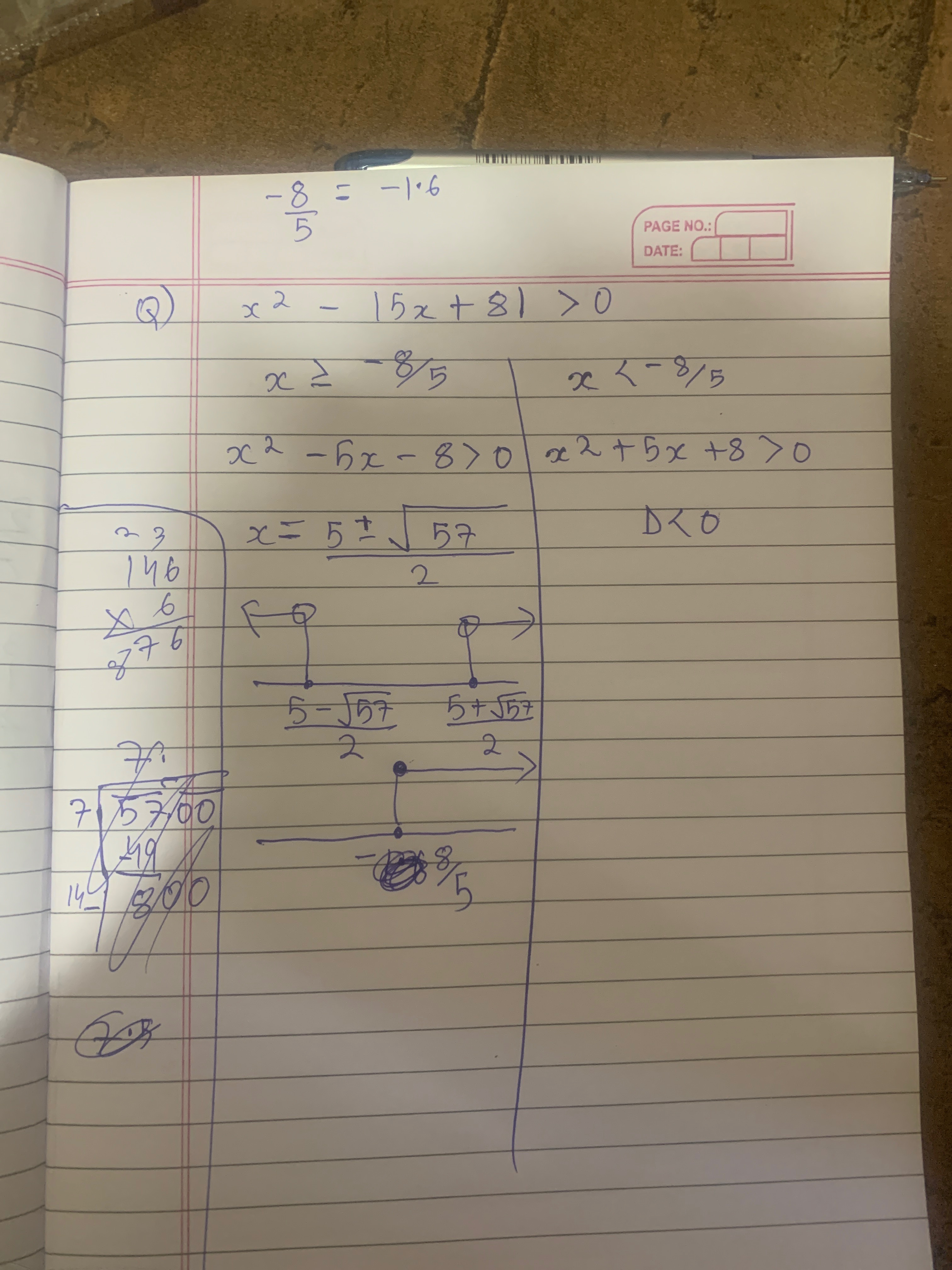
Question: $x^2 - 15x+81 > 0$...
x2−15x+81>0
(−∞,∞)
Solution
The given inequality is x2−15x+81>0. To solve this quadratic inequality, we consider the quadratic function f(x)=x2−15x+81. This is a parabola that opens upwards since the coefficient of x2 is 1>0. We find the discriminant of the quadratic equation x2−15x+81=0. The discriminant is given by D=b2−4ac, where a=1, b=−15, and c=81. D=(−15)2−4(1)(81)=225−324=−99. Since the discriminant D<0, the quadratic equation x2−15x+81=0 has no real roots. Since the parabola opens upwards (a>0) and has no real roots, the entire parabola lies above the x-axis. This means that the value of the quadratic expression x2−15x+81 is always positive for all real values of x. Therefore, the inequality x2−15x+81>0 is true for all real numbers x.
The solution set is (−∞,∞).
