Question

Four spheres of diameter $2a$ and mass $M$ are placed with their centres on the four corners of a square of side $b$. Then moment of inertia of the system about an axis about one of the sides of the square is
(A) $M{a^2} + 2M{b^2}$
(B) $M{a^2}$
(C) $M{a^2} + 4M{b^2}$
(D) $\dfrac{8}{5}M{a^2} + 2M{b^2}$

Answer 1

A system consists of four spheres of diameter $2a$ and mass $M$ placed at four corners of a square of side $b$. You are asked to find the moment of inertia of this system. Now, in order to solve this question, what you do is take the moment of inertia of the spheres about suitable axes and apply parallel axis theorem appropriately if required and add all the moments of inertia in order to find the moment of inertia of the system. By adding what is meant is that, you have to take a sphere individually, find its moment of inertia and finally add all the moments of inertia.

Complete step by step answer:
The system is as shown in the figure:

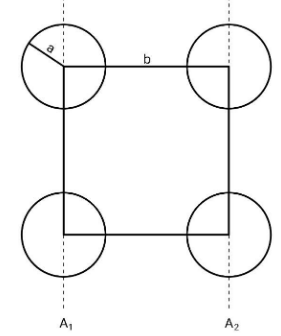
The four spheres of diameter $2a$ or radius $a$ are placed at the corners of the square of side $b$. You are supposed to find the moment of inertia of the whole system about the axis ${A_2}$.Let us consider the first sphere which is the one at the top left corner. The moment of inertia of the sphere about the axis ${A_1}$ is given by ${I_1}^1 = \dfrac{2}{5}M{a^2}$. We want the moment of inertia of this sphere about the axis ${A_2}$, hence, we apply the parallel axis theorem.

Parallel theorem states that the moment of inertia of an object about an axis is equal to the sum of moment of inertia about a parallel axis passing through the centre of mass of the object and the product of mass of the object and square of the distance between the parallel axes. Mathematically, $I = {I_{cm}} + M{d^2}$.In our case, the moment of inertia of the sphere about the axis ${A_2}$ will be
{I_1} = {I_1}^1 + M{d^2} \\\ \Rightarrow{I_1} = \dfrac{2}{5}M{a^2} + M{b^2} \\\
Similarly, as the bottom left sphere is identical to sphere both physically and according to position, the moment of inertia of the bottom left sphere will be equal to,
${I_2} = \dfrac{2}{5}M{a^2} + M{b^2}$

Now, for the spheres on the right side of the square, the moment of inertia of both will be same and will be equal to ${I_3} = {I_4} = \dfrac{2}{5}M{a^2}$.Now, the moment of inertia of the system will be the sum of all the moment of inertias, that is,
{I_{system}} = {I_1} + {I_2} + {I_3} + {I_4} \\\ \Rightarrow{I_{system}} = \dfrac{2}{5}M{a^2} + M{b^2} + \dfrac{2}{5}M{a^2} + M{b^2} + \dfrac{2}{5}M{a^2} + \dfrac{2}{5}M{a^2} \\\ \therefore{I_{system}} = \dfrac{8}{5}M{a^2} + 2M{b^2} \\\
Therefore, the moment of inertia of the system about an axis about one of the sides of the square is $\dfrac{8}{5}M{a^2} + 2M{b^2}$.

Hence, option D is correct.

Note: Whenever you are asked to find the moment of inertia of a system, you can find the moment of inertia of individual components of the system and then sum it up in order to find the moment of inertia of the whole system. You need to memorize the moment of inertia of various shapes and objects such as cylinder, solid sphere, hollow sphere, square and rectangular lamina, disc and ring. Always keep in mind that when you are given just a sphere, consider it as a solid sphere by default.