Question

Four small point objects are located at the corners of a square of side L. Each object has a charge q. Find an expression for the electric potentials for location on the axes that goes through the centre of square and perpendicular to its surface.

Answer 1

Hint : In electrostatic physics. Electric potential is the amount of energy in the form of work done needed to move a unit test positive charge from one reference point to another point. It’s denoted by $V = k\dfrac{q}{r}$ where $k = \dfrac{1}{{4\pi { \in _0}}}$ is the proportionality constant of electrostatic force and $r$ is the distance the electric charge $q$ is moved. Electric potential is a scalar quantity and is added using rules of scalar algebra.

Complete step-by-step solution:
Let us consider a square having vertices A, B, C and D and on these vertices are placed four objects having same charge $q$ and the length of side of the square ABCD is $L$ as shown in the diagram.
Let P be the point above the centre of the square ABCD at a height of $z$ and ‘O’ be the centre of the square.

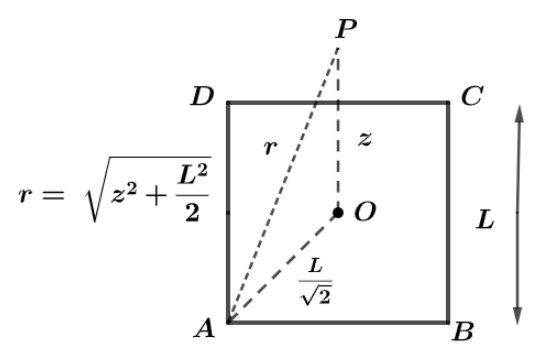
Now, from diagram we can see that, the distance $OP = z$ and $OA = \dfrac{{Diagonal}}{2}$ where,
The length of the diagonal of the square of side $L$ is $\sqrt 2 L$ .
Hence, side $OA = \dfrac{L}{{\sqrt 2 }}$
As, we can see from the symmetry that all four charges at corners of square ABCD have the same distance to point P and this distance say $r$ can be calculated as:
$r = \sqrt {{{(OA)}^2} + {{(OP)}^2}}$
Or
$r = \sqrt {{z^2} + \dfrac{{{L^2}}}{2}}$ .
Now the distance $r = \sqrt {{z^2} + \dfrac{{{L^2}}}{2}}$ is the same for all four same charges having charge of $q$ .
From the definition of electric potential,
Electric potential due to one charge at a distance of $r = \sqrt {{z^2} + \dfrac{{{L^2}}}{2}}$ is given by:
$V = k\dfrac{q}{{\sqrt {{z^2} + \dfrac{{{L^2}}}{2}} }}$
So, electric potential due to all four charges will be:
${V_{net}} = 4k\dfrac{q}{{\sqrt {{z^2} + \dfrac{{{L^2}}}{2}} }}$
Or
${V_{net}} = \dfrac{q}{{\pi { \in _0}\sqrt {{z^2} + \dfrac{{{L^2}}}{2}} }}$
Hence, the magnitude of electric potential at a point perpendicular to the surface of square above a height of $z$ is ${V_{net}} = \dfrac{q}{{\pi { \in _0}\sqrt {{z^2} + \dfrac{{{L^2}}}{2}} }}$ .

Note: It should be remembered that, the centre of a square is a point of intersection of its two diagonals and Electric Potential is a scalar quantity while electric field is position derivative of electric potential and it’s a vector quantity. The SI units of electric potential is $Nm{C^{ - 1}}$ . The numerical value of proportionality constant $k = \dfrac{1}{{4\pi { \in _0}}}$ is $9 \times {10^9}N{m^2}{C^{ - 2}}$ .