Question

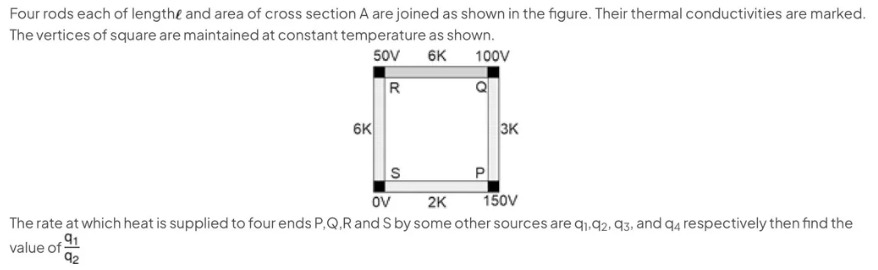
Four rods each of length $\ell$ and area of cross section A are joined as shown in the figure. Their thermal conductivities are marked. The vertices of square are maintained at constant temperature as shown.

The rate at which heat is supplied to four ends P, Q, R and S by some other sources are $q_1, q_2, q_3$, and $q_4$ respectively then find the value of $\frac{q_1}{q_2}$

Answer 1

3

Answer 2

The problem describes a square frame made of four rods with different thermal conductivities. The vertices of the square are maintained at constant temperatures. We are asked to find the ratio of the rate of heat supplied at vertex P to the rate of heat supplied at vertex Q by some external sources.

Let the vertices be denoted by R, Q, P, S in counter-clockwise order, starting from the top left. The temperatures at the vertices are given as: $T_R = 50$ $T_Q = 100$ $T_P = 150$ $T_S = 0$

The thermal conductivities of the rods are: Rod RS: $K_{RS} = 6K$ Rod RQ: $K_{RQ} = 6K$ Rod QP: $K_{QP} = 3K$ Rod SP: $K_{SP} = 2K$

Let the length of each rod be $\ell$ and the area of cross-section be A. The thermal resistance of a rod is given by $R_{th} = \frac{\ell}{KA}$. Let $R_0 = \frac{\ell}{KA}$. Then the thermal resistances of the rods are: $R_{RS} = \frac{\ell}{6KA} = \frac{R_0}{6}$ $R_{RQ} = \frac{\ell}{6KA} = \frac{R_0}{6}$ $R_{QP} = \frac{\ell}{3KA} = \frac{R_0}{3}$ $R_{SP} = \frac{\ell}{2KA} = \frac{R_0}{2}$

The rate of heat flow from a point with temperature $T_1$ to a point with temperature $T_2$ through a rod with thermal resistance $R_{th}$ is given by $Q = \frac{T_1 - T_2}{R_{th}}$.

In steady state, the temperature at each vertex is constant. This means the net rate of heat flow into each vertex from the connected rods, plus the rate of heat supplied by the external source, must be zero. Let $q_i$ be the rate of heat supplied by the external source to vertex $i$. Let $H_{in, i}$ be the net rate of heat flow into vertex $i$ from the connected rods. Then, in steady state, $q_i + H_{in, i} = 0$, so $q_i = -H_{in, i}$.

At vertex P, the connected rods are QP and SP. The rate of heat flow from Q to P is $Q_{QP} = \frac{T_Q - T_P}{R_{QP}} = \frac{100 - 150}{R_0/3} = \frac{-50}{R_0/3} = \frac{-150}{R_0}$. The rate of heat flow from S to P is $Q_{SP} = \frac{T_S - T_P}{R_{SP}} = \frac{0 - 150}{R_0/2} = \frac{-150}{R_0/2} = \frac{-300}{R_0}$. The net rate of heat flow into P from the rods is $H_{in, P} = Q_{QP} + Q_{SP} = \frac{-150}{R_0} + \frac{-300}{R_0} = \frac{-450}{R_0}$. The rate of heat supplied to P by the external source is $q_1 = -H_{in, P} = -(\frac{-450}{R_0}) = \frac{450}{R_0}$.

At vertex Q, the connected rods are RQ and QP. The rate of heat flow from R to Q is $Q_{RQ} = \frac{T_R - T_Q}{R_{RQ}} = \frac{50 - 100}{R_0/6} = \frac{-50}{R_0/6} = \frac{-300}{R_0}$. The rate of heat flow from P to Q is $Q_{PQ} = \frac{T_P - T_Q}{R_{QP}} = \frac{150 - 100}{R_0/3} = \frac{50}{R_0/3} = \frac{150}{R_0}$. The net rate of heat flow into Q from the rods is $H_{in, Q} = Q_{RQ} + Q_{PQ} = \frac{-300}{R_0} + \frac{150}{R_0} = \frac{-150}{R_0}$. The rate of heat supplied to Q by the external source is $q_2 = -H_{in, Q} = -(\frac{-150}{R_0}) = \frac{150}{R_0}$.

We need to find the value of $\frac{q_1}{q_2}$. $\frac{q_1}{q_2} = \frac{450/R_0}{150/R_0} = \frac{450}{150} = 3$.

Let's also calculate $q_3$ and $q_4$ for completeness. At vertex R, the connected rods are RQ and RS. The rate of heat flow from Q to R is $Q_{QR} = \frac{T_Q - T_R}{R_{RQ}} = \frac{100 - 50}{R_0/6} = \frac{50}{R_0/6} = \frac{300}{R_0}$. The rate of heat flow from S to R is $Q_{SR} = \frac{T_S - T_R}{R_{RS}} = \frac{0 - 50}{R_0/6} = \frac{-50}{R_0/6} = \frac{-300}{R_0}$. The net rate of heat flow into R from the rods is $H_{in, R} = Q_{QR} + Q_{SR} = \frac{300}{R_0} + \frac{-300}{R_0} = 0$. The rate of heat supplied to R by the external source is $q_3 = -H_{in, R} = 0$.

At vertex S, the connected rods are RS and SP. The rate of heat flow from R to S is $Q_{RS} = \frac{T_R - T_S}{R_{RS}} = \frac{50 - 0}{R_0/6} = \frac{50}{R_0/6} = \frac{300}{R_0}$. The rate of heat flow from P to S is $Q_{PS} = \frac{T_P - T_S}{R_{SP}} = \frac{150 - 0}{R_0/2} = \frac{150}{R_0/2} = \frac{300}{R_0}$. The net rate of heat flow into S from the rods is $H_{in, S} = Q_{RS} + Q_{PS} = \frac{300}{R_0} + \frac{300}{R_0} = \frac{600}{R_0}$. The rate of heat supplied to S by the external source is $q_4 = -H_{in, S} = -\frac{600}{R_0}$. This means heat is being removed from S.

The value of $\frac{q_1}{q_2} = \frac{450/R_0}{150/R_0} = 3$.