Question

Four resistance $P$ , $Q$ , $R$ and $X$ formed a Wheatstone bridge. The bridge is balanced when $R = 100\Omega$ . If $P$ and $Q$ are interchanged, the bridge balances for $R = 121\Omega$ . The value of $X$ is:
(A) $100\Omega$
(B) $200\Omega$
(C) $300\Omega$
(D) $110\Omega$

Answer 1

Hint To solve this question we have to use the two conditions given in the question. We should first calculate the ratio of resistance $\dfrac{P}{Q}$ in both the cases and then using this ratio we can easily calculate the unknown resistance by putting the ratio obtained in any one of the conditions.

Formula Used: The formula used in this solution is given by
$\Rightarrow \dfrac{P}{Q} = \dfrac{R}{S}$
Where the four resistances $P$ , $Q$ , $R$ and $X$ form a Wheatstone bridge

Complete step by step answer
For a Wheatstone bridge given as in the figure below,

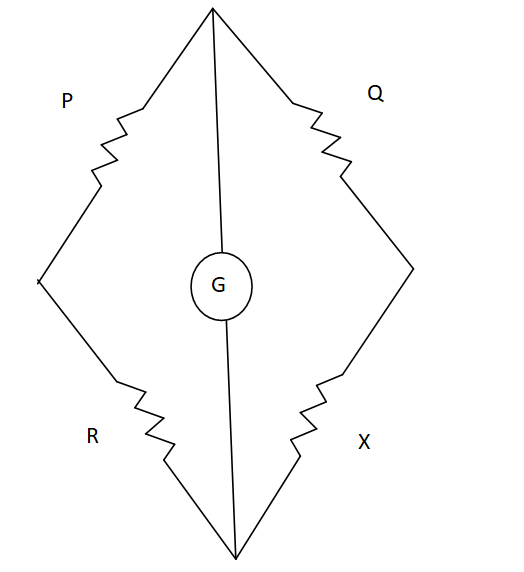
We know that,
$\Rightarrow \dfrac{P}{Q} = \dfrac{R}{X}$
Here, we obtain a balanced point for $R = 100\Omega$
SO, we get the ratio of $\dfrac{P}{Q}$ as,
$\Rightarrow \dfrac{P}{Q} = \dfrac{{100}}{X}$
This gives us $X$ as,
$\Rightarrow X = 100\dfrac{Q}{P}$
Now, if we interchange $P$ and $Q$ , we get the new Wheatstone bridge as,

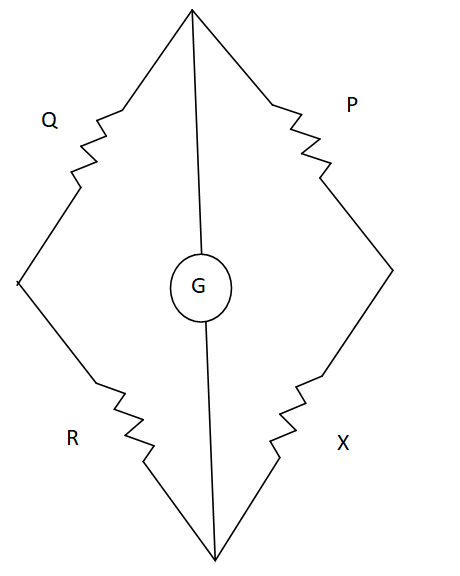
In this condition of the Wheatstone bridge, we get a balance point at $R = 121\Omega$
So, we get,
$\Rightarrow \dfrac{P}{Q} = \dfrac{R}{X} \\\ \Rightarrow \dfrac{Q}{P} = \dfrac{{121}}{X} \\\$
This gives us $X$ as,
$X = 121\dfrac{P}{Q}$
Now equating both the equation, we get,
$\Rightarrow 100\dfrac{Q}{P} = 121\dfrac{P}{Q} \\\ \Rightarrow \dfrac{{{Q^2}}}{{{P^2}}} = \dfrac{{121}}{{100}} \\\$
Thus, we get the ratio of $\dfrac{P}{Q}$ as
$\Rightarrow \dfrac{Q}{P} = \dfrac{{11}}{{10}} \\\ \Rightarrow \dfrac{P}{Q} = \dfrac{{10}}{{11}} \\\$
Now putting this value in any of the first two equations, we can get $X$ . So, now if we put the ratio in the first condition we get,
$\Rightarrow X = 100\left( {\dfrac{{11}}{{10}}} \right) \\\ \Rightarrow X = 110 \\\$
$\therefore$ Option (D) is the correct option out of the given options.

Note
A Wheatstone bridge uses a galvanometer and is derived from the concept of a meter bridge. So, using the basics of Meter-Bridge to calculate the unknown resistance of the Wheatstone is another method of solving the problem. But here it is of prime importance that we remember the order in which the resistances are put in the circuit.