Question

Four points $a,b,c$ and $d$ are set at equal distance from the center of a dipole as shown in the figure. The electrostatic potential ${V_a},{V_b},{V_c}$ and ​ ${V_d}$ would satisfy the following relation:

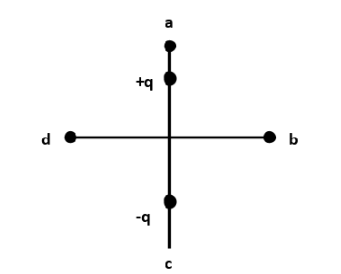
A. ${V_a} > {V_b} > {V_c} > {V_d}$
B. ${V_a} > {V_b} = {V_d} > {V_c}$
C. ${V_a} = {V_c} > {V_b} = {V_d}$
D. ${V_b} = {V_d} > {V_a} > {V_c}$

Answer 1

It is given that four points $a,b,c$ and $d$ are set at equal distance from the center of a dipole. Then the expression for electrostatic potential of a charge placed at a point distant $r$ from the origin is given by $V = \dfrac{1}{{4\pi {\varepsilon _0}k}}\dfrac{q}{r}$ where, ${\varepsilon _0}$ is the permittivity of vacuum, $r$ is the distance of the charge and $q$ is the charge (either positive or negative).
Electrostatic potential due to positive source charge is positive and negative source charge is negative.

Formula Used:
Electrostatic potential of a charge placed at a point distant $r$ from the origin is given by
$V = \dfrac{1}{{4\pi {\varepsilon _0}k}}\dfrac{q}{r}$

Complete step by step solution:
$a,b,c$ and $d$ are the four points. Let the electrostatic potential generated by them be and ${V_d}$ respectively. Let the distance of positive charge $+ q$ and negative charge $- q$ be from the center of the dipole be $l$ . Let the four points $a,b,c$ and $d$ be set at equal distance $r$ from the center of a dipole.

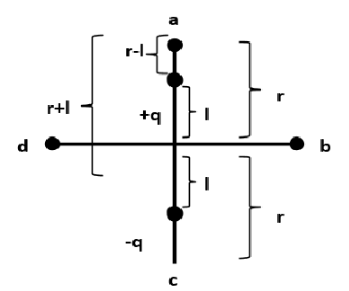
So, the distance of charge point $a$ from charge $+ q$ is $= r - l$ , and that from charge $- q$ is $= r \+ l$ . The value of electrostatic potential ${V_a}$ due to charge $+ q$ will be
${V_a} = \dfrac{1}{{4\pi {\varepsilon _0}k}}\dfrac{{ + q}}{{(r - l)}}$ or ${V_a} = \dfrac{q}{{4\pi {\varepsilon _0}k}}\dfrac{1}{{(r - l)}}$ $\to (1)$
And that due to charge $- q$ will be
${V_a} = \dfrac{1}{{4\pi {\varepsilon _0}k}}\dfrac{{ - q}}{{(r + l)}}$ or ${V_a} = \dfrac{q}{{4\pi {\varepsilon _0}k}}\dfrac{{ - 1}}{{(r + l)}}$ $\to (2)$
The total potential at point $a$ will be (Adding equations (1) and (2) )
$\Rightarrow {V_a} = \dfrac{q}{{4\pi {\varepsilon _0}k}}\left[ {\dfrac{1}{{(r - l)}} - \dfrac{1}{{(r + l)}}} \right] \\\ \Rightarrow \dfrac{1}{{4\pi {\varepsilon _0}k}}\left[ {\dfrac{{(r + l) - (r - l)}}{{(r - l)(r + l)}}} \right] \\\ \therefore {V_a} = \dfrac{1}{{4\pi {\varepsilon _0}k}}\left[ {\dfrac{{2l}}{{{r^2} - {l^2}}}} \right] \to (3)$

Similarly, the distance of charge point $c$ from charge $+ q$ is $= r + l$ , and that from charge $- q$ is $= r - l$ .

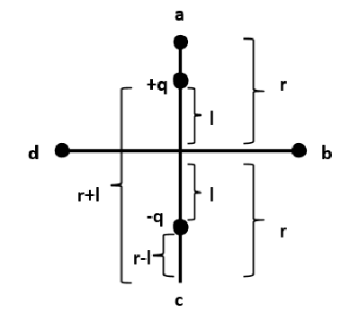
The value of electrostatic potential ${V_c}$ due to charge $+ q$ will be
${V_c} = \dfrac{1}{{4\pi {\varepsilon _0}k}}\dfrac{{ + q}}{{(r + l)}}$ or ${V_c} = \dfrac{q}{{4\pi {\varepsilon _0}k}}\dfrac{1}{{(r + l)}}$ $\to (4)$
And that due to charge $- q$ will be
${V_c} = \dfrac{1}{{4\pi {\varepsilon _0}k}}\dfrac{{ - q}}{{(r - l)}}$ or ${V_c} = \dfrac{q}{{4\pi {\varepsilon _0}k}}\dfrac{{ - 1}}{{(r - l)}}$ $\to (5)$
The total potential at point $a$ will be (Adding equations (4) and (5) )
$\Rightarrow {V_c} = \dfrac{q}{{4\pi {\varepsilon _0}k}}\left[ {\dfrac{1}{{(r + l)}} - \dfrac{1}{{(r - l)}}} \right]$
$\Rightarrow \dfrac{1}{{4\pi {\varepsilon _0}k}}\left[ {\dfrac{{(r - l) - (r + l)}}{{(r + l)(r - l)}}} \right]$ \therefore {V_c} = \dfrac{1}{{4\pi {\varepsilon _0}k}}\left[ {\dfrac{{ - 2l}}{{{r^2} - {l^2}}}} \right] \to (6) \\\
According to equation (3) and equation (6), the magnitude of electrostatic potential is the same for points $a$ and $c$ . Therefore, ${V_a} = {V_c}$ .
Points $b$ and $d$ are equidistant from both the charges, positive as well as negative. Therefore, the electrostatic potential ${V_b}$ and ${V_d}$ will be zero. Thus, ${V_b} = {V_d}$ . Since, ${V_a}$ and ${V_c}$ are greater than zero, therefore ${V_a} = {V_c} > {V_b} = {V_d}$

Hence, option (C) is the correct answer.

Note: The electrostatic potential at ${V_b}$ and ${V_d}$ is taken as zero since points $b$ and $d$ are equidistant from both the positive and negative charges. This can also be worked by applying the formula.

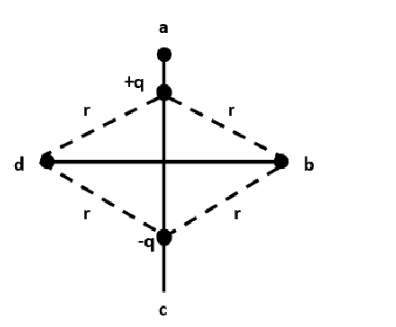
Let the distance of points $b$ and $d$ from the charges be $r$ (Refer the diagram below). Then, the electrostatic potential ${V_b}$ will be
${V_b} = \dfrac{1}{{4\pi {\varepsilon _0}k}}\dfrac{{ + q}}{r}$ or ${V_b} = \dfrac{q}{{4\pi {\varepsilon _0}k}}\dfrac{1}{r}$ $\to (7)$
And that due to charge $- q$ will be
${V_b} = \dfrac{1}{{4\pi {\varepsilon _0}k}}\dfrac{{ - q}}{r}$ or ${V_a} = \dfrac{q}{{4\pi {\varepsilon _0}k}}\dfrac{{ - 1}}{r}$ $\to (8)$
The total potential at point $a$ will be (Adding equations (7) and (8) )
\Rightarrow {V_b} = \dfrac{q}{{4\pi {\varepsilon _0}k}}\left[ {\dfrac{1}{r} - \dfrac{1}{r}} \right] \\\
\Rightarrow \dfrac{1}{{4\pi {\varepsilon _0}k}}\left[ 0 \right] \\\
\therefore {V_b} = 0 \\\
Similarly, ${V_d} = 0$
Thus, electrostatic potential is zero at points $b$ and $d$ .