Question

Four point masses lie at the corners of a rectangle of side 3m and 4m as shown in the figure. Take M kg. The diagonal joining 4M and 2M axis 1. The other diagonal in axis 2, then:

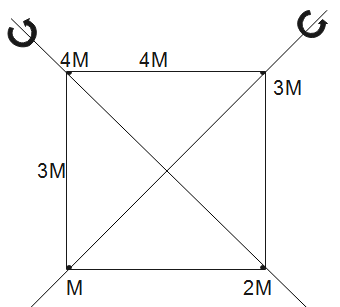
a). Moment of inertia of the system about axis 1 is 23kg meter square
b). Moment of inertia of the system about axis 1 is 26kg meter square
c). Moment of inertia of the system about axis 2 is 44kg meter square
d). Moment of inertia of the system about axis 2 is 34kg meter square

Answer 1

In this question, we will directly use the formula of Pythagoras theorem, which gives the relation between hypotenuse, base, and perpendicular of a right-angle triangle. Further, substituting the given values will help us get the required answer. Also, we will discuss the inertia and the law of inertia for our better understanding.
Formula used:
${p^2} + {b^2} = {h^2}$

Complete step by step solution:
Here, by using the Pythagoras theorem, we get:

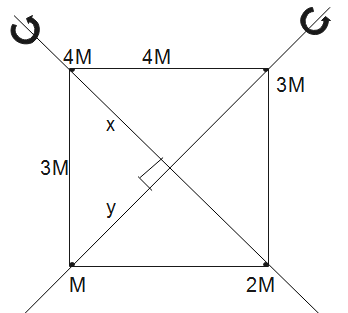
${x^2} + {y^2} = 9$
$\Rightarrow {y^2} = 9 - {x^2}.........(1)$
Also, by applying Pythagoras theorem, we have:
${(5 - x)^2} + {y^2} = 16$
Now, putting the value of y in above equation and further solving, we get:
${(5 - x)^2} + (9 - {x^2}) = 16$
$\Rightarrow {x^2} - 10x + 25 + 9 - {x^2} = 16$
$\Rightarrow x = 1.8$
So, now we can find the value of y, by putting the value of x in equation (1), we get:
${y^2} = 9 - {(1.8)^2}$
$\Rightarrow y = 2.4$
Now, as we know the moment of inertia I the ability of an object or body to continue to be in its state of motion. Here, we calculate moment of inertia for axis 1:
$\sum {M_r^2} = M \times {\left( {2.4} \right)^2} + 3M \times {\left( {2.4} \right)^2}$
$\Rightarrow \sum {M_r^2} = 4 \times {\left( {2.4} \right)^2}$
$\Rightarrow \sum {M_r^2} = 23.04 \approx 23kg{m^2}$
Similarly, we will find moment of inertia for axis 2:
$\sum {M_r^2} = 4M \times {\left( {2.4} \right)^2} + 2M \times {\left( {2.4} \right)^2}$
$\Rightarrow \sum {M_r^2} = 6 \times {\left( {2.4} \right)^2}$
$\therefore \sum {M_r^2} = 34.56kg{m^2}$
Therefore, we get the required answer for the given two axis and the correct options are a) and d) i.e. the moment of inertia of the system about axis 1 is $23kg{m^2}$ and moment of inertia of the system about axis 2 is $34.56kg{m^2}$.

Additional information: As we know Newton’s first law of motion states that an object continues to be in rest or in motion in a particular direction until and unless any external force is applied on it, this is also known as law of inertia.
Also, we know that inertia is defined as the tendency of an object to remain at rest or in motion; inertia is related to mass of an object.
As we know, force is simply any push or pull. Here the S.I unit of force is given by Newton and this is represented by N. Now, the term acceleration is defined as the rate of change of the velocity of an object or body. The acceleration is measured in meters per Second Square.
Also, we know that there are three laws of motion which are given by Newton. Now, these three laws of motion give relation between an object's motion and the forces acting on it during the motion or in rest.
When we see the first law of motion, this law states that an object or body continues to be in rest or in motion in a particular direction until and unless any external force is applied on the object or body.
Now, when we see the second law of motion, according to this law, the force on an object is equal to its mass times its acceleration. The second law also tells us the relation between momentum and force.
Now, the last one i.e., in the third law of motion, according to this every action has an equal and opposite reaction.

Note: We should now remember that the Pythagoras theorem is only valid for right angle triangles not for any other shape. Also, there is a very small difference between the force applied and the pressure applied on an object. We should also note that pressure is given as the force experienced by an object per unit area.