Question

Four persons A, B, C and D initially at the corners of a square of side of length d. If every person starts moving with same speed v such that each one faces the other always, the person will meet after time
1. $\dfrac{\sqrt{2} \mathrm{d}}{\mathrm{v}}$
2. $\dfrac{d}{2 v}$
3. $\dfrac{d}{\sqrt{2 v}}$
4. $\dfrac{d}{v}$

Answer 1

We should know that velocity is defined as the rate change of displacement per unit time. Speed in a specific direction is also known as velocity. Velocity is equal to displacement divided by time. Speed, being a scalar quantity, is the rate at which an object covers distance. The average speed is the distance which is a scalar quantity per time ratio. On the other hand, velocity is a vector quantity; it is direction-aware. An object which moves in the negative direction has a negative velocity. If the object is slowing down then its acceleration vector is directed in the opposite direction as its motion in this case. Based on this we have to solve this question.

Complete step by step answer
Intuitively, it may seem like the four people will never meet, because the person they are moving towards is always moving away from them. The key is that while the person they are moving towards is moving, they are not actually moving away from the person chasing them. In fact, the person moving away will always move perpendicular to the line between them and the person chasing them, so they never get further away from their pursuer. On the other hand, the person chasing them is always moving towards them at speed v. Therefore, the distance between these two people decreases at speed $\mathrm{v},$ and the time it takes for them to meet is $\dfrac{d}{v}$.

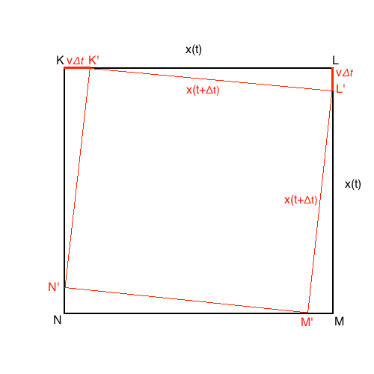
For the more mathematically inclined, this may not seem like much of a proof, so here is a way to show this with a little bit of calculus:
First, let's look at what would happen if all of the people were to move in their initial direction (set only by the initial positions of A, B, C, D for a time $t=\Delta t$
It is not hard to show that the red shape must also be a square. This is not surprising but important for our calculation. Let's take the square at an arbitrary time $t,$ with side lengths $x(t) .$ Notice that we have a right triangle with side lengths $x(t)-v \Delta t, v \Delta t,$ and $x(t+\Delta t) .$ Using the Pythagorean theorem, we obtain the equation:
$x(t+\Delta t)^{2}=(x(t)-v \Delta t)^{2}+(v \Delta t)^{2}$
Expanding the squared equations, we get:
$x(t+\Delta t)^{2}=x(t)^{2}-2 x(t) v \Delta t+2(v \Delta t)^{2}$
Now, let $\alpha(t)=x(t)^{2}:$
$\alpha(t+\Delta t)=\alpha(t)-2 \sqrt{\alpha(t)} v \Delta t+2(v \Delta t)^{2}$
More algebra, move $\alpha(t)$ over, divide by $\Delta t$ $\dfrac{\alpha(t+\Delta t)-\alpha(t)}{\Delta t}=-2 \sqrt{\alpha(t)} v+2 v^{2} \Delta t$
Now notice if we let $\Delta t$ go to 0 (which represents continuous motion), the left side is just a derivative:
$\dfrac{d \alpha(t)}{d t}=-2 \sqrt{\alpha(t)} v$
Now this is just a differential equation that is easy to solve with separation of variables:
$\dfrac{d \alpha}{\sqrt{\alpha(t)}}=-2 v d t$
Note, our integral over $\alpha(t)$ will go from $d^{2}$ to $x(t)^{2}$. $\int_{d^{2}}^{x(t)^{2}} \dfrac{d \alpha(t)}{\sqrt{\alpha(t)}}=\int_{0}^{t}-2 v d t$
Now this is just a differential equation that is easy to solve with separation of variables:
$\dfrac{d \alpha}{\sqrt{\alpha(t)}}=-2 v d t$
Note, our integral over $\alpha(t)$ will go from $d^{2}$ to $x(t)^{2}$. $\int_{d^{2}}^{x(t)^{2}} \dfrac{d \alpha(t)}{\sqrt{\alpha(t)}}=\int_{0}^{t}-2 v d t$
$(2 \sqrt{\alpha(t)})_{d^{2}}^{x(t)^{2}}=-2 v t$
$|x|-|d|=-v t$
Now we can solve for $t$ when $x=0$ (d is assumed to be positive, so we drop the absolute value):
$t=\dfrac{d}{v}$

So the correct answer is option 4.

Note: We should know that if an object's speed or velocity is increasing at a constant rate then we say it has uniform acceleration. The rate of acceleration is constant. If a car speeds up then slows down then speeds up it doesn't have uniform acceleration. The instantaneous acceleration, or simply acceleration, is defined as the limit of the average acceleration when the interval of time considered approaches 0. It is also defined in a similar manner as the derivative of velocity with respect to time. If an object begins acceleration from rest or a standstill, its initial time is 0. If we get a negative value for acceleration, it means the object is slowing down. The acceleration of an object is its change in velocity over an increment of time. This can mean a change in the object's speed or direction. Average acceleration is the change of velocity over a period of time. Constant or uniform acceleration is when the velocity changes the same amount in every equal time period.