Solveeit Logo
Login

Question

Question: Four particles of masses \(m_A=m, m_B=2m, m_C=3m\) and \(m_D=4m\) are at the corners of a square. ...

Four particles of masses mA=m,mB=2m,mC=3mm_A=m, m_B=2m, m_C=3m and mD=4mm_D=4m are at the
corners of a square. They have accelerations of equal magnitude with directions as shown. The acceleration of the center of mass of the particles is

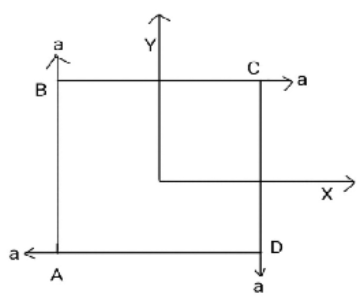
A.a5(i^−j^) B.a5(i^+j^) C.Zero D.a(i^+j^) \begin{aligned} & A.\dfrac{a}{5}(\hat{i}-\hat{j}) \\\ & B.\dfrac{a}{5}(\hat{i}+\hat{j}) \\\ & C.\text{Zero} \\\ & D.a(\hat{i}+\hat{j}) \\\ \end{aligned}

Explanation

Solution

Hint: Here we just need to know the mathematical formula of the center of mass of a system of particles. Also, we need to write the accelerations in vector form. We can assume the origin to be at the center of the square (not centre of mass). Then after simply putting the accelerations in the formula, the acceleration of centre of mass is found.

Formula used:
A⃗=∑mia⃗i∑mi\vec A=\dfrac{\sum m_i \vec a_i}{\sum m_i}

Complete step-by-step solution:
The magnitude of acceleration of the four particles are the same. But they have different directions.
Hence the accelerations of the different particles in vector form is given by,
a⃗A=−ai^\vec a_A=-a \hat i
a⃗B=aj^\vec a_B=a \hat j
a⃗C=ai^\vec a_C=a \hat i
a⃗D=−aj^\vec a_D=-a \hat j
(Considering their directions as given in the question)
Now center of mass of a system of particles is mathematically defined as,
R⃗=∑mir⃗i∑mi\vec R=\dfrac{\sum m_i \vec r_i}{\sum m_i}
Where the mim_i is the mass of the i-th particle and r⃗i\vec r_i is its position.
Now differentiating this twice, we just obtain the acceleration of the center of mass of the
particle. Hence, we get
A⃗=∑mia⃗i∑mi=∑mia⃗i10m=2mai^−2maj^10m=a5(i^−j^)\vec{A}=\dfrac{\sum{{{m}_{i}}}{{{\vec{a}}}_{i}}}{\sum{{{m}_{i}}}}=\dfrac{\sum{{{m}_{i}}}{{{\vec{ a}}}_{i}}}{10m}=\dfrac{2ma\hat{i}-2ma\hat{j}}{10m}=\dfrac{a}{5}(\hat{i}-\hat{j})
Hence, option A is the correct answer.

Additional information:
The center of mass of a system of particles is independent of the choice of the origin. But its position vector may have different expressions for different frames of reference. Again, the position of the origin is not so important while dealing with acceleration, we just need the magnitude and direction of the acceleration.

Note: Remember the following things:
1. While calculating the summation on the numerator, always multiply the mass with
corresponding acceleration.
2. Moreover take care of the signs of the different terms as well.
3. You have to do the summation of the denominator and the numerator differently.