Question

Four particles of masses m, 2m, 3m and 4m are placed at the corners of a square of side of length ‘a’. The gravitational force on a particle of mass m placed at the centre of the square is
A) $4\sqrt 2 \dfrac{{G{m^2}}}{{{a^2}}}$
B) $3\sqrt 2 \dfrac{{G{m^2}}}{{{a^2}}}$
C) $2\sqrt 2 \dfrac{{G{m^2}}}{{{a^2}}}$
D) $\sqrt 2 \dfrac{{G{m^2}}}{{{a^2}}}$

Answer 1

Recall Newton’s law of universal gravitation. According to this law, every object attracts other objects in the universe. The force of attraction points in a straight line between the centre of both the objects. It is directly proportional to the mass of the objects and inversely proportional to the square of distance between them.

Complete step by step solution:
The formula for gravitational force is given by
$F = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}$
Where G is the gravitational force
${m_1}$ is the mass of the first object
${m_2}$ is the mass of the second object
And ‘r’ is the distance between them
Given that the length of each side of the square is = a
The distance of each corner from the centre will be $= \dfrac{a}{{\sqrt 2 }}$

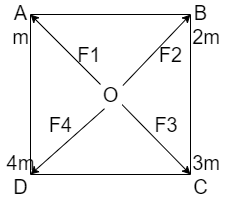
The gravitational force on point O due to point A is given by
$\Rightarrow {F_1} = \dfrac{{Gmm}}{{{{(\dfrac{a}{{\sqrt 2 }})}^2}}} = \dfrac{{2G{m^2}}}{{{a^2}}}$
Similarly, the gravitational force on point O due to point B is written as
$\Rightarrow {F_2} = \dfrac{{G(2m)(m)}}{{{{(\dfrac{a}{{\sqrt 2 }})}^2}}} = \dfrac{{4G{m^2}}}{{{a^2}}}$
The gravitational force on point O due to point C will be
$\Rightarrow {F_3} = \dfrac{{G(3m)(m)}}{{{{(\dfrac{a}{{\sqrt 2 }})}^2}}} = \dfrac{{6G{m^2}}}{{{a^2}}}$
The gravitational force on point O due to point D will be
$\Rightarrow {F_4} = \dfrac{{G(4m)(m)}}{{{{(\dfrac{a}{{\sqrt 2 }})}^2}}} = \dfrac{{8G{m^2}}}{{{a^2}}}$
The net force of ${F_1}$and ${F_3}$on point O is given by
$\Rightarrow {F_{13}} = {F_3} - {F_1}$
$\Rightarrow {F_{13}} = \dfrac{{6G{m^2}}}{{{a^2}}} - \dfrac{{2G{m^2}}}{{{a^2}}} = \dfrac{{4G{m^2}}}{{{a^2}}}$
Similarly, the force of ${F_2}$and${F_4}$on point O is given by
$\Rightarrow {F_{24}} = {F_4} - {F_2}$
$\Rightarrow {F_{24}} = \dfrac{{8G{m^2}}}{{{a^2}}} - \dfrac{{4G{m^2}}}{{{a^2}}} = \dfrac{{4G{m^2}}}{{{a^2}}}$
The magnitude of net force on point O is given by
$\Rightarrow F = \sqrt {{{({F_{13}})}^2} + {{({F_{24}})}^2}}$
$\Rightarrow F = \sqrt {{{(\dfrac{{4G{m^2}}}{{{a^2}}})}^2} + {{(\dfrac{{4G{m^2}}}{{{a^2}}})}^2}}$
$\Rightarrow F = \sqrt {2.\dfrac{{4{G^2}{m^4}}}{{{a^4}}}}$
$\Rightarrow F = 2\sqrt 2 \dfrac{{G{m^2}}}{{{a^2}}}$

Option C is the right answer.

Note: It is important to note that since the force of gravitation is directly proportional to the mass of the object, so an object with more mass will have a large force of gravitation. But it varies inversely with the square of distance, so if the distance is doubled the force of gravitation will decrease by 4 times and so on.