Question

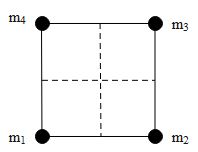
Four particles of masses${{m}_{1}}=2m$, ${{m}_{2}}=4m$, ${{m}_{3}}=m$and ${{m}_{4}}$ are placed at four corners of a square. What should be the value of ${{m}_{4}}$, so that the centre of mass of all the four particles are exactly at the centre of the square?

Answer 1

The central mass will be present at the centre of the square with the coordinates being half the length of the side of a square. The x and y coordinates equals the sum of the product of the masses and distances of all the masses present at the corners by the sum of the masses of all the masses present at the corners of the square.

Complete answer:
From the given information, we have the data as follows.
Four particles of masses${{m}_{1}}=2m$, ${{m}_{2}}=4m$, ${{m}_{3}}=m$and ${{m}_{4}}$ are placed at four corners of a square.
Let the side of the square be ‘a’.
We are asked to find the mass 4, such that the central mass lies at the centre of the square.
Let us consider the coordinate system first to solve this problem.

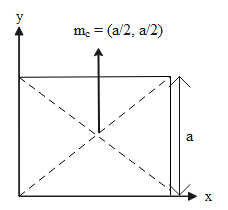
The x and y coordinates of the central mass are $({{x}_{c}},{{y}_{c}})=\left( \dfrac{a}{2},\dfrac{a}{2} \right)$.
Now consider the x-axis distance of the central mass.
${{x}_{c}}=\dfrac{{{m}_{1}}{{a}_{1}}+{{m}_{2}}{{a}_{2}}+{{m}_{3}}{{a}_{3}}+{{m}_{4}}{{a}_{4}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}$
Substitute the values in the above formula.
$\dfrac{a}{2}=\dfrac{2m\times 0+4m\times a+m\times a+{{m}_{4}}\times 0}{2m+4m+m+{{m}_{4}}}$
Continue further computation.

& \dfrac{a}{2}=\dfrac{4m\times a+m\times a}{7m+{{m}_{4}}} \\\ & \Rightarrow \dfrac{a}{2}=\dfrac{5ma}{7m+{{m}_{4}}} \\\ & \Rightarrow 7m+{{m}_{4}}=2\times 5m \\\ & \therefore {{m}_{4}}=2\times 5m-7m \\\ \end{aligned}$$ Thus, the value of the mass 4 is, $$\begin{aligned} & {{m}_{4}}=10m-7m \\\ & \therefore {{m}_{4}}=3m \\\ \end{aligned}$$ Similarly, consider the y-axis distance of the central mass. $${{y}_{c}}=\dfrac{{{m}_{1}}{{a}_{1}}+{{m}_{2}}{{a}_{2}}+{{m}_{3}}{{a}_{3}}+{{m}_{4}}{{a}_{4}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}$$ Substitute the values in the above formula. $$\dfrac{a}{2}=\dfrac{2m\times 0+4m\times 0+m\times a+{{m}_{4}}\times a}{2m+4m+m+{{m}_{4}}}$$ Continue further computation. $$\begin{aligned} & \dfrac{a}{2}=\dfrac{m\times a+{{m}_{4}}\times a}{7m+{{m}_{4}}} \\\ & \Rightarrow \dfrac{1}{2}=\dfrac{m+{{m}_{4}}}{7m+{{m}_{4}}} \\\ & \Rightarrow 7m+{{m}_{4}}=2m+2{{m}_{4}} \\\ & \therefore 7m-2m=2{{m}_{4}}-{{m}_{4}} \\\ \end{aligned}$$ Thus, the value of the mass 4 is, $$\begin{aligned} & 5m={{m}_{4}} \\\ & \therefore {{m}_{4}}=5m \\\ \end{aligned}$$ As, a total of 2 values exist for the same mass. thus, not a single value of mass 4 exists for which the central mass of the system lies at the centre of the square, that is, at a distance of $$\left( \dfrac{a}{2},\dfrac{a}{2} \right)$$ $$\therefore $$ The single value of $${{m}_{4}}$$does not exist so that the centre of mass of all the four particles are exactly at the centre of the square. **Note:** The x coordinate equals the sum of the product of the masses and distances along the x-axis of all the masses present at the corners by the sum of the masses of all the masses present at the corners of the square. Similarly, the y coordinate equals the sum of the product of the masses and distances along the y-axis of all the masses present at the corners by the sum of the masses of all the masses present at the corners of the square.