Question

Four particles of masses 1 kg, 2 kg, 3 kg and 4 kg are placed at the four vertices A, B, C and D, respectively of a square of side 1 m. Find the position of the centre of mass of the particles.

Answer 1

The centre of mass of the system of particles is defined as the position where the all the mass of the system of particles is considered to be. It is the point where if linear force is applied on the system then there will not be any angular acceleration.

Formula used: The formula of the centre of mass is given by,
$\Rightarrow {\vec r_{cm}} = \dfrac{{{m_1}{{\vec r}_1} + {m_2}{{\vec r}_2} + \cdot \cdot \cdot \cdot \cdot + {m_n}{{\vec r}_n}}}{{{m_1} + {m_2} \cdot \cdot \cdot \cdot {m_n}}}$
Where centre of mass is ${\vec r_{cm}}$ and mass of different particles are ${m_1}$, ${m_2}$ etc. and the different vector positions are ${\vec r_1}$, ${\vec r_2}$ and etc.

Complete step by step solution:
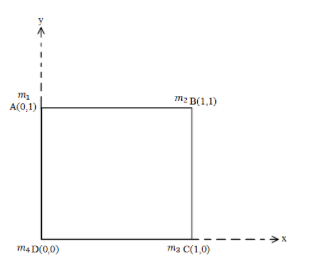
It is given in the problem that four particles of masses 1 kg, 2 kg, 3 kg and 4 kg are placed at the four vertices A, B,C and D, respectively of a square of side 1 m and we need to find the position of the centre of mass of the particles.
The mass of the four particles are${m_1} = 1kg$, ${m_2} = 2kg$, ${m_3} = 3kg$ and ${m_4} = 4kg$. Also the position vector of the particles are ${\vec r_1} = 0\hat i + 0\hat j$, ${\vec r_2} = \hat i$, ${\vec r_3} = \hat j$ and ${\vec r_4} = \hat i + \hat j$.

The formula of the centre of mass is given by,

$\Rightarrow {\vec r_{cm}} = \dfrac{{{m_1}{{\vec r}_1} + {m_2}{{\vec r}_2} + \cdot \cdot \cdot \cdot \cdot + {m_n}{{\vec r}_n}}}{{{m_1} + {m_2} \cdot \cdot \cdot \cdot {m_n}}}$

Where centre of mass is ${\vec r_{cm}}$ and mass of different particles are ${m_1}$, ${m_2}$ etc. and the different vector positions are ${\vec r_1}$, ${\vec r_2}$ and etc.

Replacing the mass and the position vector in the above formula we get,

$\Rightarrow {\vec r_{cm}} = \dfrac{{{m_1}{{\vec r}_1} + {m_2}{{\vec r}_2} + \cdot \cdot \cdot \cdot \cdot + {m_n}{{\vec r}_n}}}{{{m_1} + {m_2} \cdot \cdot \cdot \cdot {m_n}}}$
$\Rightarrow {\vec r_{cm}} = \dfrac{{1 \times \left( {0\hat i + 0\hat j} \right) + 2\left( {\hat i} \right) + 3\hat j + 4\left( {\hat i + \hat j} \right)}}{{1 + 2 + 3 + 4}}$
$\Rightarrow {\vec r_{cm}} = \dfrac{{2\hat i + 4\hat i + 3\hat j + 4\hat j}}{{10}}$
$\Rightarrow {\vec r_{cm}} = \dfrac{{6\hat i + 7\hat j}}{{10}}$
$\Rightarrow {\vec r_{cm}} = 0 \cdot 6\hat i + 0 \cdot 7\hat j$.

So the centre of mass of the system of particles is equal to${\vec r_{cm}} = 0 \cdot 6\hat i + 0 \cdot 7\hat j$.

Note: The students are advised to understand and remember the formula of the centre of mass as it is very useful in solving problems like this. The centre of mass can be present outside the physical bodies. The centre of mass is an inertial frame and it is at rest compared to the origin of the coordinate system.