Question

Four particles of equal mass ${{M}}$ moves along a circle of radius ${{R}}$ under the action of their mutual gravitational attraction. Find the speed of each particle.

Answer 1

First of all, write the given quantities. Here, the required centripetal force in order to move the respective masses is provided by the mutual gravitational attraction. So, equate the centripetal force with Newton’s universal law of gravitation i.e. ${{F = }}\dfrac{{{{G}}{{{m}}_1}{{{m}}_2}}}{{{{{R}}^{{2}}}}}$ where ${{{m}}_{{1}}}{{ = }}$ mass of the first body, ${{{m}}_{{2}}}{{ = }}$ mass of the second body, ${{R = }}$ distance between the two bodies and ${{G = }}$ universal gravitational constant.

Complete step by step solution:
Given: Four particles having mass ${{M}}$each moves along a circular track having radius ${{R}}$
To find: The speed of each particle
Let us name all the particles in such a way shown in figure below (particle 1, particle 2, particle 3 and particle 4)

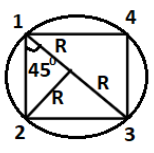
When two particles having mass ${{M}}$ and ${{m}}$. The distance between both the particles is ${{R}}$. Then the force of attraction is given by the formula
${{F = }}\dfrac{{{{G}}{{{m}}_{{1}}}{{{m}}_{{2}}}}}{{{{{R}}^{{2}}}}}...{{(i)}}$
Force of attraction between particle 1 and particle 4 is given by using relation (i),
$\Rightarrow {{{F}}_{{{14}}}}{{ = }}\dfrac{{{{G}}{{{M}}^2}}}{{{{2}}{{{R}}^{{2}}}}}$
Since the distance between the particle 1 and particle 4 is ${{R + R = 2R}}$
And the mass of particle 1 and particle 4 is ${{M}}$
Force of attraction between particle 1 and particle 2 is given by using relation (i),
$\Rightarrow {{{F}}_{{{12}}}}{{ = }}\dfrac{{{{G}}{{{M}}^2}}}{{{{2}}{{{R}}^{{2}}}}}$
Since the distance between the particle 1 and particle 2 is ${{R + R = 2R}}$
And the mass of particle 1 and particle 2 is ${{M}}$
Now resultant of these two forces i.e. ${{{F}}_{{{14}}}}$ and ${{{F}}_{{{12}}}}$ is $\dfrac{{\sqrt {{2}} {{GM}}}}{{{{4}}{{{R}}^{{2}}}}}$.
Force of attraction between particle 1 and particle 3 is given by using relation (i),
$\Rightarrow {{{F}}_{{{13}}}}{{ = }}\dfrac{{{{G}}{{{M}}^2}}}{{{{2}}{{{R}}^{{2}}}}}$
Since the distance between the particle 1 and particle 3 is ${{R + R = 2R}}$
And the mass of particle 1 and particle 3 is ${{M}}$
Net force is given by
$\Rightarrow {{{F}}_{{{net}}}}{{ = }}\dfrac{{\sqrt {{2}} {{G}}{{{M}}^{{2}}}}}{{{{2}}{{{R}}^{{2}}}}}{{ + }}\dfrac{{{{G}}{{{M}}^{{2}}}}}{{{{4}}{{{R}}^{{2}}}}}$
Centripetal force, ${{{F}}_{{C}}}{{ = }}\dfrac{{{{M}}{{{v}}^{{2}}}}}{{{R}}}$
The required centripetal force in order to move the respective masses is provided by the mutual gravitational attraction.
Now equating centripetal force with net force, we get
$\Rightarrow \dfrac{{{{M}}{{{v}}^{{2}}}}}{{{R}}}{{ = }}\dfrac{{\sqrt {{2}} {{G}}{{{M}}^{{2}}}}}{{{{2}}{{{R}}^{{2}}}}}{{ + }}\dfrac{{{{G}}{{{M}}^{{2}}}}}{{{{4}}{{{R}}^{{2}}}}}$
On further solving, we get
$\Rightarrow \dfrac{{{{{v}}^{{2}}}}}{1}{{ = }}\dfrac{{{{GM}}}}{{{R}}}{{ }}\left( {\dfrac{{2\sqrt 2 + 1}}{4}} \right) \\\ \therefore {{v = }}\sqrt {\dfrac{{{{GM}}}}{{{R}}}{{ }}\left( {\dfrac{{{{2}}\sqrt {{2}} {{ + 1}}}}{{{4}}}} \right)}$

Thus, the speed of each particle will be ${{ }}\sqrt {\dfrac{{{{GM}}}}{{{R}}}{{ }}\left( {\dfrac{{{{2}}\sqrt {{2}} {{ + 1}}}}{{{4}}}} \right)}$.

Note: Centripetal force is a force that makes an object or a body to move in a curved path. The direction to the motion of the body is always orthogonal towards a fixed point. According to Newton, centripetal force is a force according to which bodies are drawn towards a point to a centre.