Question

Four particles, each of mass M, move along a circle of radius R, under the action of their mutual gravitational attraction. The speed of particle is
A. $\dfrac{{GM}}{R}$
B. $\sqrt {2\sqrt 2 \dfrac{{GM}}{R}}$
C. $\sqrt {\dfrac{{GM}}{R}(2\sqrt 2 + 1)}$
D. $\sqrt {\dfrac{{GM}}{R}\left( {\dfrac{{2\sqrt 2 + 1}}{4}} \right)}$

Answer 1

Hint: The resultant gravitational force acting on each body will act as the centripetal force for the circular motion. Equate the expression of centripetal force for one mass with the resultant gravitational forces acting on the same mass due to the other 3 masses in motion.

Complete answer:

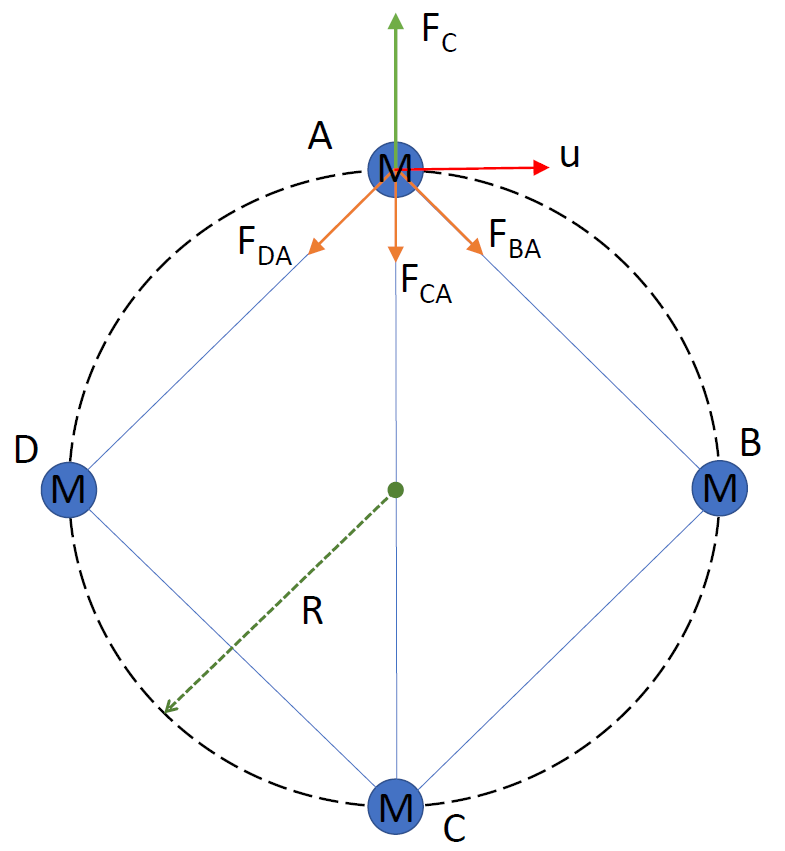
Four particles of masses M form a square ABCD inscribed in the circular path. R is the radius of the circle. Based on Newton’s law of gravitation, every mass exerts a force of gravity which is directly proportional to the product of their masses and inversely proportional to the square of distance between their centres. Here we will consider the balance of forces on the particle at A.
Resultant Force of Gravitation:
Since the radius of the circle is R distance between masses at A and C, $AC = 2R$. Since ABCD is a square, the length of its diagonal is equal to the diameter of the circle in which it is inscribed. Length of the diagonal of a square is $\sqrt 2$ times the length of its sides. Therefore,
$AD = AB = \dfrac{1}{{\sqrt 2 }}AC = \dfrac{1}{{\sqrt 2 }} \times 2R = \sqrt 2 R$
Since Masses at D and B are equidistant from A, force of gravitational attraction is also of the same magnitude. The expressions are as follows:
${F_{DA}} = {F_{BA}} = \dfrac{{G{M^2}}}{{{{(\sqrt 2 R)}^2}}} = \dfrac{{G{M^2}}}{{2{R^2}}}$. The direction of the forces are given in the figure. Net force on mass at A due to these forces is as follows ($\theta = {90^ \circ }$ between the forces):
$\Rightarrow {F_A} = \sqrt {F_{DA}^2 + F_{BA}^2 + 2{F_{DA}}{F_{BA}}\cos \theta }$
$\Rightarrow {F_A} = \sqrt {2F_{DA}^2} = \sqrt 2 {F_{DA}} = \sqrt 2 \dfrac{{G{M^2}}}{{2{R^2}}} = \dfrac{{G{M^2}}}{{\sqrt 2 {R^2}}}$
The expression for force of gravitational attraction on mass at A due to mass at C is given as:
${F_{CA}} = \dfrac{{G{M^2}}}{{{{(2R)}^2}}} = \dfrac{{G{M^2}}}{{4{R^2}}}$
${F_A}$ and ${F_{CA}}$ are along same direction so the resultant gravitational force is simply their arithmetic sum and is given as follows:
$\Rightarrow {F_G} = {F_{CA}} + {F_A} = \dfrac{{G{M^2}}}{{4{R^2}}} + \dfrac{{G{M^2}}}{{\sqrt 2 {R^2}}}$
$\Rightarrow {F_G} = \dfrac{{G{M^2}}}{{{R^2}}}\left( {\dfrac{{1 + 2\sqrt 2 }}{4}} \right)$ (1)
This is directed toward the centre of the circle.
Centripetal force:
Let $u$ be the velocity of the particle along the circle. Then the inward, towards the centre of the circle, centripetal force on the particle is given by
${F_C} = \dfrac{{M{u^2}}}{R}$ (2)
For the circular motion to sustain, the resultant gravitational force will act as the centripetal force. Thus from (1) and (2), we get,
$\Rightarrow {F_C} = {F_G}$
$\Rightarrow \dfrac{{G{M^2}}}{{{R^2}}}\left( {\dfrac{{1 + 2\sqrt 2 }}{4}} \right) = \dfrac{{M{u^2}}}{R}$
$\Rightarrow {u^2} = \dfrac{{GM}}{{4R}}(1 + 2\sqrt 2 )$
$\Rightarrow u = \sqrt {\dfrac{{GM}}{R}\left( {\dfrac{{2\sqrt 2 + 1}}{4}} \right)}$
Comparing the options with the final answer, we conclude that option D is the correct one.

Note: Be careful while simplifying terms within the square root terms. It is very likely to make mistakes, especially with the power of each variable. A check whether you are incorrect is comparing the components of gravitational forces due masses on either side. They should be opposite and equal. Thus there should not be any component of force in the direction of velocity at any point on the motion.