Solveeit Logo
Login

Question

Question: Four particles each of mass \(m\) are located at the vertices of a square of edge \(L\). What is the...

Four particles each of mass mm are located at the vertices of a square of edge LL. What is the gravitational potential of the system at the center of the square?

Explanation

Solution

Gravitational potential at any point is defined as the work to be done to bring a unit mass from infinity to that point.
Gravitational potential due to a point mass MM at a distance xx units is inversely proportional to xx.
Use the formula of gravitational potential to obtain potential at centre of square due to each of the masses and then sum up to obtain the gravitational potential of the system.

Formula used:
Gravitational potential, V(x)=−GMxV(x)=\dfrac{-GM}{x}

Complete step-by-step answer:
The gravitational potential V at distance x from a point mass of mass M can be defined as the work W that needs to be done by an external agent to bring a unit mass in from infinity to that point. Mathematically,
V(x)=Wm=1m∫∞xF.dx=1m∫∞x−GmMx2dx=−GMxV(x)=\dfrac{W}{m}=\dfrac{1}{m}\int\limits_{\infty }^{x}{\mathbf{F}.d\mathbf{x}}=\dfrac{1}{m}\int\limits_{\infty }^{x}{\dfrac{-GmM}{{{x}^{2}}}dx}=\dfrac{-GM}{x}
Where G is the gravitational constant and F is the gravitational force.
According to the question, four particles each of mass mm are located at the vertices of a square of edge LL as shown in figure below.


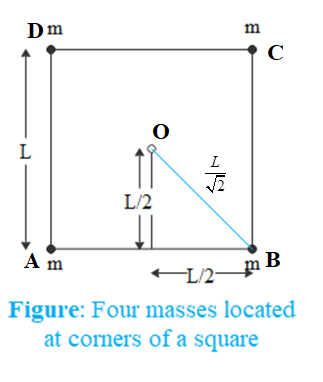
Each mass is at distance L2\dfrac{L}{\sqrt{2}} from centre O of the square. Therefore,
Gravitational potential at O due to mass m at A
VA=−GmL/2=−Gm2L{{V}_{A}}=\dfrac{-Gm}{L/\sqrt{2}}=\dfrac{-Gm\sqrt{2}}{L}
Similarly, gravitational potential at O due to masses at B, C and D will also be the same since the distance of O from all the vertices of the square is the same.
Hence, VA=VB=VC=VD=−Gm2L{{V}_{A}}={{V}_{B}}={{V}_{C}}={{V}_{D}}=\dfrac{-Gm\sqrt{2}}{L}
Potential is a scalar quantity. The net potential at O will be the sum of potentials due to all four masses. Therefore,
VO=VA+VB+VC+VD=−4GmL/2{{V}_{O}}={{V}_{A}}+{{V}_{B}}+{{V}_{C}}+{{V}_{D}}=\dfrac{-4Gm}{L/\sqrt{2}}
We conclude that, the gravitational potential of the system at the center of square is −4Gm2L\dfrac{-4Gm\sqrt{2}}{L}

Note: Always use a negative sign in the expression for gravitational potential. Since, gravitational force is always attractive. That is why gravitational potential has negative signs. Value of gravitational potential reaches zero at infinity. Gravitational potential increases with distance.