Question

Four particles each of mass M and equidistant from each other, move along a circle of radius under the acting of their mutual gravitational attraction. The speed of each particle is:
(A) $\sqrt {\dfrac{{GM}}{R}(1 + 2\sqrt 2 )}$
(B) $\dfrac{1}{2}\sqrt {\dfrac{{GM}}{R}(1 + 2\sqrt 2 )}$
(C) $\sqrt {\dfrac{{GM}}{R}}$
(D) $\sqrt {2\sqrt 2 \dfrac{{GM}}{R}}$

Answer 1

To solve this question, we have to calculate the centripetal force on the masses, as the masses are moving in a circular motion. Then, we need to equate this force with the gravitational force acting on each mass.

Formula used:
The formulae used in this solution is given as,
${F_G} = G\dfrac{{Mm}}{{{R^2}}}$
Here, ${F_G}$ is the gravitational force between the 2 bodies, $G$ is the Universal Gravitational Constant, $M$ is the mass of the first body, $m$ is the mass of the second body, and $R$ is the distance between the two bodies.
${F_C} = \dfrac{{M{v^2}}}{R}$
Here, ${F_C}$ is the centripetal force acting on the body and $v$ is the velocity of the body.

Complete step by step solution:
Let us first draw a figure representing the conditions given in the question.

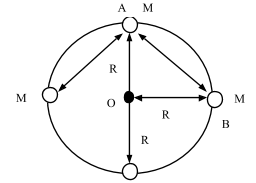
From the figure, we can now apply Pythagoras theorem on the triangle AOB, to get,
$A{O^2} + O{B^2} = A{B^2}$
This gives us, the distance between the two masses as,
$AB = \sqrt {{R^2} + {R^2}}$
$\Rightarrow AB = R\sqrt 2$
Now, if we calculate, effective force on one particle due to other particles, the same force will be acting on all the other masses because all the particles have the same mass and are equidistant. So, let us calculate the force on a particle at A.
Thus, we get,
${F_G} = {F_{AB}} + {F_{AC}} + {F_{AD}}$
From the figure, we can infer that the distance between points B and D from point A are the same. So,
${F_{AB}} = {F_{AD}}$
Now, we can resolve the forces through the figure,

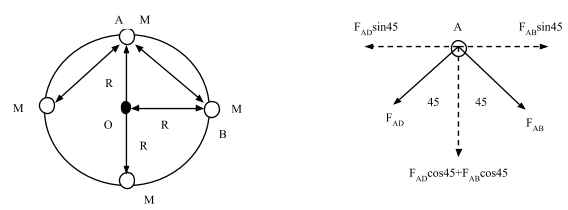
Now, from the resolution of forces we observe that the horizontal forces cancel out and the vertical components add up. So, we can write the net force on A as,
${F_G} = {F_{AB}} + {F_{AC}} + {F_{AD}}$
$\Rightarrow {F_G} = {F_{AB}}\cos 45 + {F_{AC}} + {F_{AD}}\cos 45$
Now since ${F_{AB}} = {F_{AD}} = F(say)$
So, we can write,
${F_G} = 2F\cos 45 + {F_{AC}}$
$\Rightarrow {F_G} = 2\left( {\dfrac{{G{M^2}}}{{{{\left( {R\sqrt 2 } \right)}^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) + \left( {\dfrac{{G{M^2}}}{{{{(2R)}^2}}}} \right)$
So, we can calculate the effective force on A as,
${F_G} = \left( {\dfrac{{G{M^2}}}{{{R^2}\sqrt 2 }}} \right) + \left( {\dfrac{{G{M^2}}}{{4{R^2}}}} \right)$
$\Rightarrow {F_G} = \dfrac{{G{M^2}}}{{{R^2}}}\left( {\dfrac{{4 + \sqrt 2 }}{{4\sqrt 2 }}} \right)$
But since the particles also traverse on a circular path, they also experience a centripetal force towards the center. This centripetal force is balanced by the gravitational force experienced by the particle due to other particles. Hence, we can write,
${F_C} = {F_G}$
$\Rightarrow \dfrac{{M{v^2}}}{R} = {F_G}$
Thus, we can write,
$\dfrac{{M{v^2}}}{R} = \dfrac{{G{M^2}}}{{{R^2}}}\left( {\dfrac{{4 + \sqrt 2 }}{{4\sqrt 2 }}} \right)$
$\Rightarrow {v^2} = \dfrac{{GM}}{{4R}}\left( {2\sqrt 2 + 1} \right)$
Thus, we get the velocity of each particle as,
$v = \sqrt {\dfrac{{GM}}{{4R}}\left( {2\sqrt 2 + 1} \right)}$

$\Rightarrow v = \dfrac{1}{2}\sqrt {\dfrac{{GM}}{R}\left( {2\sqrt 2 + 1} \right)}$
$\therefore$ Option (B) is the correct option.

Note:
While solving this question, we don’t need to worry about the position of the masses while making the calculation for the net gravitational force acting on a mass. This is because each position is symmetric with respect to the other masses, so force will be the same along the whole circle.