Question

Four particles each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is

(A) $\sqrt {\dfrac{{Gm}}{R}(1 + 2\sqrt 2 )}$
(B) $\dfrac{1}{2}\sqrt {\dfrac{{GM}}{R}(1 + 2\sqrt 2 )}$
(C) $\sqrt {\dfrac{{GM}}{R}}$
(D) $\sqrt {2\sqrt 2 \dfrac{{GM}}{R}}$

Answer 1

In particle are moving in circle then gravitational force on each particle is balanced by centripetal force i.e.,
${F_g} = {F_C} = \dfrac{{{\rm M}{u^2}}}{R}$
Where
u $=$ velocity of particle
R $=$ radius of circle
M $=$ mass of particle

Complete step by step answer:
From the figure we can easily calculate the net force on any one particle.

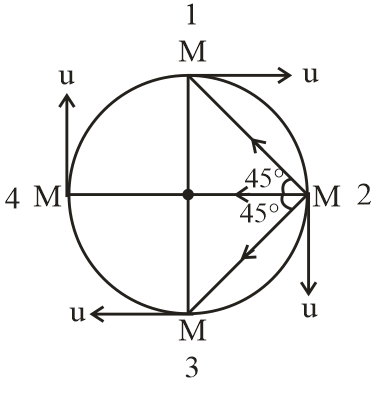
Now we can calculate the net force on particle 2 by vector component method.

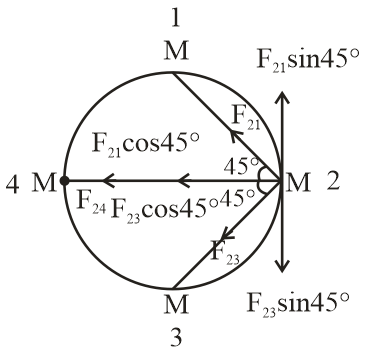
First, we resolve the 2 forces ${F_{21}}$ & ${F_{23}}$ by component method. Let the resultant of ${F_{21}}$ & ${F_{23}}$ is ${F^1}$. So, ${F^1}$ is given as by diagram
${F^1} = {F_{21}}\cos 45^\circ + {F_{23}}\cos 45^\circ$ ….(1)
Because sine components of ${F_{21}}$ & ${F_{23}}$ cancel out to each other because ${F_{21}}$ & ${F_{23}}$ having same magnitude but direction are opposite. So, the combined force of ${F_{21}}$ & ${F_{23}}$ on 2 is only due to their cosine components.
We know that gravitational force is given by
${F_g} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}$
Here r $=$ distance between mass ${m_1}$ and ${m_2}$.
So, ${F_{21}} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}$
Here r is distance between ${m_1}$ and ${m_2}$
$r = \sqrt 2 R$ and ${m_1} = {m_2} = M$
So, ${F_{21}} = \dfrac{{G{M^2}}}{{{{(\sqrt 2 R)}^2}}} = \dfrac{{G{M^2}}}{{2{R^2}}}$ …..(2)
And ${F_{23}} = \dfrac{{G{m_2}{m_3}}}{{{r^2}}}$
Here r $=$ distance between ${m_2}$ & ${m_3}$ which is $\sqrt 2 R$.
and ${m_3} = {m_2} = M$
${F_{23}} = \dfrac{{G{M^2}}}{{{{(\sqrt 2 R)}^2}}} = \dfrac{{G{M^2}}}{{2{R^2}}}$ …..(3)
From equation 1, 2 and 3
${F^1} = 2\left( {\dfrac{{G{M^2}}}{{2{R^2}}}} \right)\cos 45^\circ$
$\because$ $\cos 45^\circ = \dfrac{1}{{\sqrt 2 }}$
${F^1} = \dfrac{{G{M^2}}}{{\sqrt 2 {R^2}}}$ …..(4)
In diagram, we can easily see that the direction of ${F^1}$ and ${F_{24}}$ is same i.e., –x
So, the net force on particle 2 is
${F_2} = {F^1} + {F_{24}}$ …..(5)
Now, ${F_{24}} = \dfrac{{G{m_2}{m_4}}}{{{r^2}}}$
Here r $=$ distance between ${m_2}$ and ${m_4}$
And ${m_2} = {m_4} = M$
So, ${F_{24}} = \dfrac{{G{M^2}}}{{{{(2R)}^2}}} = \dfrac{{G{M^2}}}{{4{R^2}}}$ …..(6)
From equation 4, 5 and 6
${F_2} = \dfrac{{G{M^2}}}{{\sqrt 2 {R^2}}} + \dfrac{{G{M^2}}}{{4{R^2}}}$
${F_2} = \dfrac{{G{M^2}}}{{{R^2}}}\left( {\dfrac{1}{4} + \dfrac{1}{{\sqrt 2 }}} \right)$ …..(7)
This net force on 2 is balanced by centripetal force because the particle is moving with velocity u in circular orbit of radius R.
So, ${F_2} = \dfrac{{M{u^2}}}{R}$ …..(8)
From equation 7 & 8
$\dfrac{{M{u^2}}}{R} = \dfrac{{G{M^2}}}{{{R^2}}}\left( {\dfrac{1}{4} + \dfrac{1}{{\sqrt 2 }}} \right)$
$= \dfrac{{GM}}{R}\left( {\dfrac{{\sqrt 2 + 4}}{{4\sqrt 2 }}} \right)$
$\implies {u^2} = \dfrac{1}{4}\dfrac{{GM}}{R}\left( {1 + 2\sqrt 2 } \right)$
$\implies u = \sqrt {\dfrac{{GM}}{{4R}}\left( {1 + 2\sqrt 2 } \right)}$
$\therefore u = \dfrac{1}{2}\sqrt {\dfrac{{GM}}{R}\left( {1 + 2\sqrt 2 } \right)}$

So, the correct answer is “Option B”.

Note:
A centripetal force is a net force that acts on an object to keep it moving along a circular path. If 2 charges having distance r between them are moving in a circular path then centripetal force is balanced by electrostatic force. i.e.,
${F_e} = \dfrac{{m{v^2}}}{r} = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$