Question
Question: Four metallic plates each with surface area of one side \( A \) , are placed at a distance \( d \) f...
Four metallic plates each with surface area of one side A , are placed at a distance d from each other. The two outer plates are connected to one point A and the two other inner plates to another point B as shown in the figure. Then the capacitance of the system is:
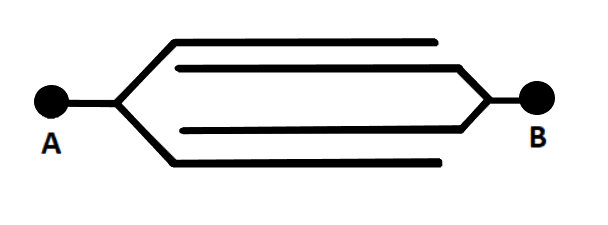
(A) dε0A
(B) d2ε0A
(C) d3ε0A
(D) d4ε0A
Solution
Hint : Capacitance is defined as the ability of plates to store energy when there will be potential difference between the plates. Here, the plates will form three capacitors when they are connected to each other. Therefore, to calculate the capacitance of the system, we will add the capacitance of each capacitor.
The formula of capacitance of each plate is given by
C=dε0A
Here, C is the capacitance, ε0 is the permittivity, A is the area of plates and d is the separation between the plates.
Complete Step By Step Answer:
Four metallic plates are connected with each other. These plates are connected in such a way they will form three capacitors, each of them will have a potential difference AB .
Now, when the capacitors will have the same potential difference, then the capacitor is said to be a parallel combination.
Now, capacitance is defined as the ability of plates to store energy when there will be potential difference between the plates. The capacitance in the plates of area A separated by a distance d from each other is given by
C=dε0A
Now, as the plates are forming three capacitors having potential difference AB , therefore, to calculate the capacitance of the system, we will calculate the capacitance of each three plate as shown below
Cnet=dε0A+dε0A+dε0A
⇒Cnet=d3ε0A
Therefore, the capacitance of the system consisting of four plates is d3ε0A
Hence, option (C) is the correct option.
Note :
We can also calculate the capacitance of the system of four plates as shown below
Cnet=3C
⇒Cnet=d3ε0A
The result is the same as that of the result calculated above. We have multiplied the capacitance by 3 because the plates are forming the combination of three capacitors.
