Question

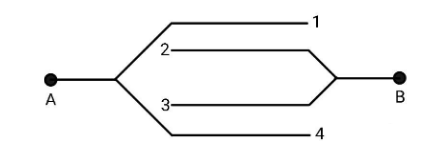
Four metallic plates each with a surface area of one side $A$, are placed at a distance $d$ from each other. The two outer plates are connected to one point $A$ and the two other inner plates to another point $B$ as shown in the figure. Then the capacitance of the system is

(A) $\dfrac{{{\varepsilon _0}A}}{d}$
(B) $\dfrac{{2{\varepsilon _0}A}}{d}$
(C) $\dfrac{{3{\varepsilon _0}A}}{d}$
(D) $\dfrac{{4{\varepsilon _0}A}}{d}$

Answer 1

You are given an arrangement of four plates and are asked to find the capacitance of the system or arrangement. When a potential difference is applied across the system, that is, points A and B are different potentials, charges will appear on the plates. The charges that will appear on the plates will follow the equation $Q = CV$, where $Q$ is the charge on one plate of a capacitor, $C$ is the capacitance and $V$ is the potential difference across the capacitor. Find the capacitors that will be formed in the system and to find the capacitance of that capacitor, use $Q = CV \to C = \dfrac{Q}{V}$. If required, use the method of equivalent capacitors for series and parallel combination.

Complete step by step answer:
You can see that the plates $1\& 4$ are at the same potential ${V_A}$ and so are the plates $2\& 3$, they are also at the same potential that is ${V_B}$. Now, let us talk about the charge’s distribution on the plates.Let the potential at point A be ${V_A} = {V_ + }$ and that at point B be${V_B} = {V_ - }$. Positive charges will appear at the plates $1\& 4$ and negative charges will appear at the plates $2\& 3$. Let the surface charge density be $\sigma = \dfrac{Q}{A}$.So, we have two capacitors, one will be including plates $1\& 2$ and the other will be including plates $3\& 4$.

First, let us consider the plates $1\& 2$. Draw a Gaussian cylinder perpendicular to the plate with one end inside the plate $1$ and the other end in between the plates $1\& 2$. The electric field will be perpendicular to the plates. Applying Gauss’s law to this closed surface, we get,
\oint {{\mathbf{E}}.\Delta {\mathbf{A}} = \dfrac{{{Q_{en}}}}{{{\varepsilon _0}}}} = \dfrac{{\sigma \Delta A}}{{{\varepsilon _0}}} \\\ \Rightarrow E\Delta A = \dfrac{{\sigma \Delta A}}{{{\varepsilon _0}}} \\\ \Rightarrow E = \dfrac{\sigma }{{{\varepsilon _0}}} = \dfrac{Q}{{A{\varepsilon _0}}} \\\
Now, the potential difference between the plates will be $V = {V_ + } - {V_ - } = - \int {{\mathbf{E}}.d{\mathbf{r}}}$. As you go from $2 \to 1$, the electric field and displacement are in opposite direction and therefore, ${\mathbf{E}}.d{\mathbf{r}} = - Edr$
$V = - \int {{\mathbf{E}}.d{\mathbf{r}}} = \int {Edr} = Ed = \dfrac{{Qd}}{{A{\varepsilon _0}}}$
As capacitance is equal to $\dfrac{Q}{V}$, therefore, $C = \dfrac{{{\varepsilon _0}A}}{d}$. Similarly, for the other capacitor, the capacitance is $C = \dfrac{{{\varepsilon _0}A}}{d}$. Here, the capacitances are in parallel as the positives and the negative plates of both the capacitors are having common points. Therefore, the equivalent capacitance of these two capacitors will be $C = {C_1} + {C_2} = \dfrac{{{\varepsilon _0}A}}{d} + \dfrac{{{\varepsilon _0}A}}{d} = \dfrac{{2{\varepsilon _0}A}}{d}$.Hence, the capacitance of the system is $\dfrac{{2{\varepsilon _0}A}}{d}$.

Hence, option B is correct.

Note: You should always remember Gauss's law which states that the electric flux through a closed surface is given by the charge enclosed by the closed surface divided by the permittivity. Also, whenever you are needed to find the capacitance of any capacitor, use the equation $Q = CV$.