Question

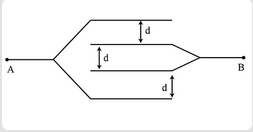
Four metallic plates are arranged as shown in the figure. If $d$ is the distance between each plate then capacitance of the given system between points $A$ and $B$ is: (given $d < < A$)

A) $\dfrac{{{\varepsilon _0}A}}{d}$
B) $\dfrac{{2{\varepsilon _0}A}}{d}$
C) $\dfrac{{3{\varepsilon _0}A}}{d}$
D) $\dfrac{{4{\varepsilon _0}A}}{d}$

Answer 1

Look for the number of capacitance in the given diagram and for the type of connection between the capacitance.

Complete step by step solution:
We know from the question that the distance between each plate is $d$ and the area of the plate of capacitor is $A$.
We know from the figure that there are two capacitances between the point A and B and they are connected in parallel.
The capacitance of the given system between points $A$ and $B$ is,
$C = {C_1} + {C_2}$ ... (1)
We know that the expression of the capacitance of parallel plate capacitance is,
$C = \dfrac{{{\varepsilon _0}A}}{d}$
Here, ${\varepsilon _0}$ is the absolute permittivity.
We know that the distance between each plate is and their area is also the same. So the capacitance of both capacitance will be the same.
${C_1} = {C_2} = \dfrac{{{\varepsilon _0}A}}{d}$
Substitute the above expression in equation (1), we have,
$C = \dfrac{{{\varepsilon _0}A}}{d} + \dfrac{{{\varepsilon _0}A}}{d}\\\ = \dfrac{{2{\varepsilon _0}A}}{d}$
Hence, the capacitance of the given system between points $A$ and $B$ is $\dfrac{{2{\varepsilon _0}A}}{d}$ and the option (B) is correct.

Additional information: Capacitance comprises two parallel plates, which are separated by dielectric like air or insulated material. The capacitor has a tendency to store the charge of electrons. The capacitance of the capacitor is directly proportional to the distance between its plates and inversely proportional to the area of the plate.

Note: Capacitance with air as its dielectric: $C = \dfrac{{{\varepsilon _0}A}}{d}$ Capacitance with insulated material as its dielectric: $C = \dfrac{{{\varepsilon _r}{\varepsilon _0}A}}{d}.$