Question
Question: Four massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass...
Four massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass M kept on a frictionless plane as shown in the figure. If the mass M is displaced in the horizontal direction, then the frequency of the system is:
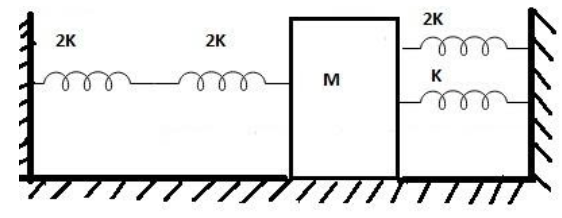
A) 2π14Mk
B) 2π1M4k
C) 2π17Mk
D) 2π17M7k
Solution
Formula for frequency is:
2π1LC1 (L is the inductor, C is the capacitor)
As per electrical and mechanical analogy conversion, in force current analogy M is the capacitor (C) and k is the reciprocal of the inductor (1/L).
Let’s find the value of k using series and parallel connections (using 1/L = k, in series connections are added with their direct connections and the parallel connection have reciprocal addition).
Complete step by step solution:
As we are provided with an inductor and capacitor in the system then we will add the reciprocal of the inductor for the series connection.
K=K1+K2
First, we will do the calculation for series connection:
⇒K1=2k1+2k1 ⇒K1=2k+2k2k×2k (Taking LCM)
⇒K1=2k2k=1k
Now, we will calculate for the springs in parallel:
⇒K2=2k11+k11 ⇒K2=2k+k=3k (in parallel connection we have to take the reciprocal of the spring constants)
Total value of K comes out to be:
⇒K=K1+K2 ⇒K=k+3k=4k
From the equation of frequency:
⇒f=2π1MK11 ⇒f=2π1MK (We have substituted the value of LC as per formula of frequency)
⇒f=2π1M4k (We have substituted the values M and K).
Hence, Option B is correct.
Note: In the question above we have used electrical to mechanical equivalent system of force current, where current is acting as the force in a mechanical system, mass as capacitor, frictional coefficient as reciprocal of R resistor, spring constant as reciprocal of L inductor, displacement as magnetic flux and velocity as voltage.
