Question

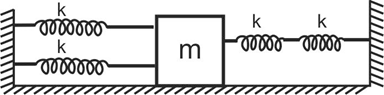
Four massless springs each of force constant $k$ are attached to a mass $m$kept on a smooth plane as shown in figure. If the mass is displaced in the horizontal direction and released, its frequency of oscillation is:

A) $\dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{{4m}}}$
B) $\dfrac{1}{{2\pi }}\sqrt {\dfrac{{4k}}{m}}$
C) $\dfrac{1}{{2\pi }}\sqrt {\dfrac{{2k}}{{5m}}}$
D) $\dfrac{1}{{2\pi }}\sqrt {\dfrac{{5k}}{{2m}}}$

Answer 1

For the given question firstly, we have to find the spring equivalent spring constant of both the sides, that is the Left-Hand Side and the Right-Hand Side. After that combine both side’s equivalency in a single equivalency by adding them. Calculate the Time Period and the after that, calculation of reciprocal of Time period gives the required frequency of oscillations.

Complete step by step solution:
As we know that according to the strategy of equivalency of spring constant-
In general, given $n$ springs added in series:
$\Rightarrow \dfrac{1}{{{k_{eq}}}} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}} + \dfrac{1}{{{k_3}}} + .... + \dfrac{1}{{{k_n}}}$
In general, given $n$ springs added in parallel
$\Rightarrow {k_{eq}} = {k_1} + {k_2} + {k_3} + .... + {k_n}$
So according to the figure, firstly finding the equivalent parallel combination of the spring (that is in the left-hand side):
$\Rightarrow {k_{eq1}} = k + k$
$\Rightarrow {k_{eq1}} = 2k$
Then finding the equivalent series combination of the spring (that is in the right-hand side):
$\Rightarrow \dfrac{1}{{{k_{eq2}}}} = \dfrac{1}{k} + \dfrac{1}{k} = \dfrac{{1 + 1}}{k} = \dfrac{2}{k}$
$\Rightarrow {k_{eq2}} = \dfrac{k}{2}$
Now, total equivalent spring constant combining both the sides, is given by:
$\Rightarrow {k_{eq}} = 2k + \dfrac{k}{2} = \dfrac{{4k + k}}{2} = \dfrac{{5k}}{2}$
Now, the time period of oscillation is given by:
$T = 2\pi \sqrt {\dfrac{m}{{{k_{eq}}}}}$
Now, we substitute equivalent spring constant as,
$\Rightarrow T = 2\pi \sqrt {\dfrac{{2m}}{{5k}}}$
As we know that the frequency is given by
$\Rightarrow f = \dfrac{1}{T}$
Now, we substitute the time period expression in the above equation,
$\Rightarrow f = \dfrac{1}{{2\pi \sqrt {\dfrac{{2m}}{{5k}}} }}$
After simplification, we get
$\therefore f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{5k}}{{2m}}}$

Thus, option $(D)$ is the correct answer.

Note: When two springs are connected in series, the result is essentially a longer and flimsier spring. When a force is applied to the combined spring, the same force is applied to each individual spring. When two springs are connected in parallel, the result is essentially two springs working together. When a force is applied to the combined spring, the force applied on each individual spring is different.