Question
Question: Four masses m,2m,3m and 4m are kept on a straight line at 0, a ,2a, and 3a as shown in figure. The r...
Four masses m,2m,3m and 4m are kept on a straight line at 0, a ,2a, and 3a as shown in figure. The radius of gyration of the system about axis AB is,
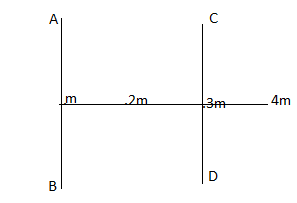
(a)2a(b)3a(c)2a(d)5a
Solution
First calculate the moment of inertia about the axis. Where the moment of inertia is the algebraic sum of the product of mass and square of distance. Thus on substituting the values of m and r we will get the moment of inertia about the axis AB. Then calculate the radius of gyration. Radius of gyration is related to the moment of inertia and the total mass of the body. That is the square of radius of gyration is the ratio of moment of inertia to the total mass.
Formula used:
Moment of inertia is given by,
I=i=1∑∞miri2 ………(1)
Here, I is the moment of inertia
m is the mass
r is the distance.
I=Mk2 …………..(2)
where, I is the moment of inertia
M is the total mass
k is the radius of gyration
Complete answer:
First we have to calculate the moment of inertia about the axis AB.
For this expand the equation (1).
That is,
I=m1r12+m2r22+...........+mnrn2 ………….(3)
where, I is the moment of inertia
m is the mass
r is the distance .
Here the equation becomes,
IAB=m1r12+m2r22+m3r32+m4r42 ……………(4)
Given that,
m1=mm2=2mm3=3mm4=4m
Also given that,
r1=0r2=ar3=2ar4=3a
Then substituting these values in equation (4) we get,
IAB=m(02)+2m(a2)+3m(2a)2+4m(3a)2
⇒IAB=2ma2+12ma2+36ma2
⇒IAB=50ma2
Then find the radius of gyration using equation (2).
I=Mk2
Here the equation becomes,
IAB=Mk2 …………(5)
We have already found the moment of inertia about the axis AB.
That is,
IAB=50ma2
M=m1+m2+m3+m4
⇒M=m+2m+3m+4m
⇒M=10m
Thus substituting the value of IAB and M we get,
50ma2=10mk2
Rearranging the equation for k2,
⇒k2=10m50ma2
⇒k2=5a2
⇒k=5a
So, the correct answer is “Option D”.
Note:
Thus the radius of gyration of a body about an axis can be also defined as the distance from the axis of a mass point whose mass is equal to the mass of the whole body and moment of inertia is equal to the moment of inertia of the body about the axis. In case of a rigid body, it depends upon the mass, shape, distribution of mass about the axis etc.
