Question

Four married couples are to be seated in a merry-go round with 8 identical seats. In how many ways can they be seated so that males and females sit alternatively?
A. 6
B. 12
C. 18
D. 24

Answer 1

A rule of thumb for problems of this kind is to seat a particular category of people and then find the number of ways by which the other category of people can occupy the remaining seats. In this manner, we’ll be able to decompose the problem to identify and consider each case of arrangement easily.

Complete step by step answer:
First of all, it is given that there are 4 males and 4 females and they are seated in a merry go round that means that they will be seated in a circular arrangement as follows:

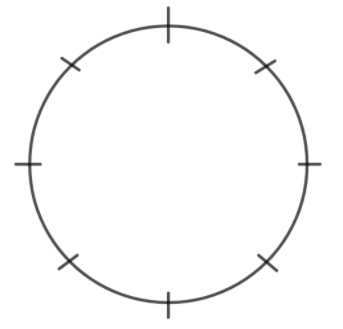
We’ll seat the males on 4 seats (out of 8) so that they sit alternatively. Observe that this can be done in the following ways:

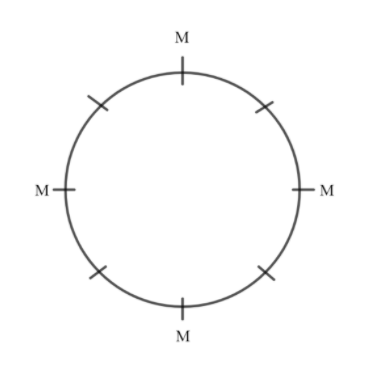
Now, observe that the 4 males can be seated in each other’s seat without affecting the condition imposed in question. The first male can interchange his seat with the second, third or fourth male (3 ways of arrangement). The second male can interchange his seat with the third or fourth male (2 ways of arrangement) and the third male can interchange his seat with the fourth male (1 way of arrangement). Observe that it is necessary to ensure that we don’t consider a particular case more than once.
Total ways in which males can be seated in each other’s seat and still sit alternatively is 3+2+1=6 ways.
Now, we introduce the females in the empty seats (represented by blanks above) so that they also sit alternatively.

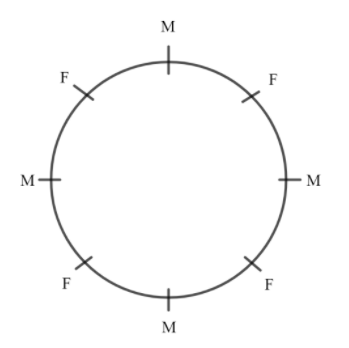
In a similar way, the 4 females can be seated in each other’s seats without affecting the condition imposed i.e. they sit alternatively. By using the above procedure, we see that the total ways of arrangement of females amongst themselves is 6.
Hence, the total number of ways in which the 4 couples can be seated so that the males and females sit alternatively is C. 12

So, the correct answer is “Option C”.

Note: Students can make a mistake while arranging the given persons as one can ignore the given circular arrangement and may arrange them in a straight line. Always draw a figure in questions like this and it will be better for understanding of the examiner. Also, explain the steps in detail as the question does not require calculations.