Question
Question: Four \( \left[ {40{\text{W}},{\text{ }}230{\text{V}}} \right] \) bulbs are connected to a \( 230{\te...
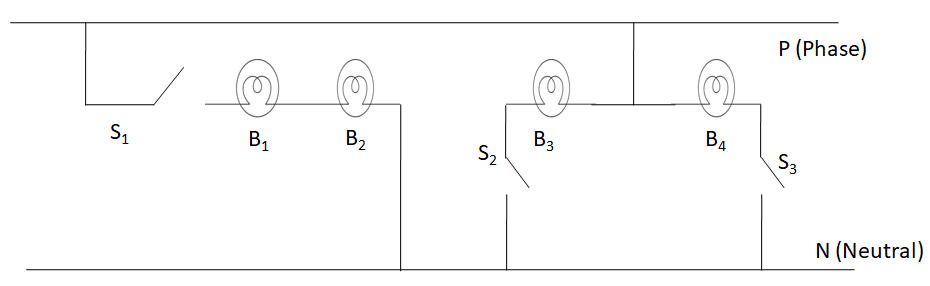
Four [40W, 230V] bulbs are connected to a 230V supply as shown below.
-Which are the bulbs connected in series?
-Which are the bulbs that can work at 40W power?
-Write two advantages of connecting household equipment in parallel.
Solution
To answer this question, we need to use the bulb rating given to find the resistance of each bulb using its relation with the power. For identifying the series and the parallel combinations, we have to see the connection of the terminals of the bulbs. After identifying the series and the parallel combinations, we can divide the voltage across each bulb to find out the maximum power.
Formula Used: The formula used in this solution is
P=RV2 , here P is the power developed across a resistance R , which is supplied to a voltage V
Complete step by step answer:
Let the resistance of the bulbs be R .
The ratings of each of the four bulbs in the given circuit of the question are
Maximum power P=40W
Voltage V=230V
We know that the power is given by
P=RV2
So the resistance is given by
R=PV2
Putting the values from the rating of the bulb, we get
R=402302
R=1322.5Ω
So the resistance of each bulb is equal to 1322.5Ω .
-We can see that the bulbs B1 and B2 connected through the switch S1 have one terminal common. The other terminal of bulb B1 is connected to the phase line, while that of the bulb B2 is connected to the neutral line. So, the bulbs B1 and B2 are connected in series between the phase and the neutral.
Hence, the answer to this part is B1 and B2.
-Considering the bulbs B1 and B2, as they are connected in series, the 230V of the supply is divided between them. The voltage is equally divided, as both the bulbs have the same resistance. So, the voltage across each bulb is
V1=2230=115V . So the maximum power across each of the bulbs B1 and B2 is given by P1=1322.51152=10W
Therefore, the maximum power which the bulbs B1 and B2 can withstand is equal to 10W . So they cannot work at 40W power.
Now, considering the bulbs B3 and B4, we can see that in both of them, one terminal is connected to the phase and the other to the neutral. Hence, they are connected in parallel. We know that the voltage is not divided in a parallel combination. So, the voltage across both of them is
V2=230V
So the maximum power across each of the bulbs B3 and B4 is given by
P2=1322.52302=40W .
Therefore, the bulbs B3 and B4 can work at 40W power.
Hence, the answer of this part is B3 and B4.
-As can be seen in b part, the parallel combination does not divide the voltage across each element. Hence, each device can work on its maximum power rating, when connected in a parallel combination with the other devices.
Also, in a series combination, if one of the elements stops working, the other elements stop working. This is because the circuit breaks at the defective element and the current stops flowing. But in a parallel combination, the current is divided among the devices. Hence, if one device stops working, the other devices are not affected.
Note:
As all the four bulbs in this question are identical, we can attempt this question without even finding the value of resistance. We can use the proportionality between the power and the voltage to directly evaluate the maximum power across each bulb.
