Question

Four identical thin rods each of mass M and length l form a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is?
A. $\dfrac{1}{3}M{{l}^{2}}$
B. $\dfrac{8}{3}M{{l}^{2}}$
C. $\dfrac{2}{3}M{{l}^{2}}$
D. $\dfrac{4}{3}M{{l}^{2}}$

Answer 1

We know the standard expression for moment of inertia of a rod along its centre. Now by applying parallel axes theorem we could find the moment of inertia of each rod along the perpendicular axis. Then we could take the sum of moment of inertia of all the four axes and thus get the required moment of inertia.

Formula used:
Parallel axes theorem,
$I={{I}_{body}}+m{{d}^{2}}$

Complete step-by-step answer:
In the question we are given four identical thin rods of mass M and length l each forming a square frame. We are asked to find the moment of inertia about an axis perpendicular to this frame and also passing through its centre.
Let the frame be placed on the x-y plane so that the moment of inertia to be found will be along the z-axis which is perpendicular to this plane.

We know the standard expression for the moment of inertia of a rod of length $l$ about its centre is given by,
$I=\dfrac{m{{l}^{2}}}{12}$ ……………………………….. (1)
Now let us recall parallel axis theorem, which states that the moment of inertia of a body about an axis parallel to the body that is passing through its center will be equal to the sum of moment of inertia of the body about the axis passing through the centre and the product of mass of the body times the square of the distance between the two axes. That is,
$I={{I}_{body}}+m{{d}^{2}}$ …………………………….. (2)
Now let us apply the parallel axis theorem for all the rods.

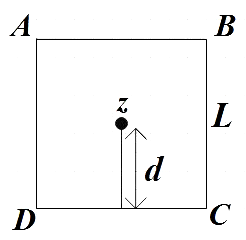
For rod AB,
${{I}_{1}}={{I}_{AB}}+m{{d}^{2}}$
From (1), ${{I}_{AB}}=\dfrac{m{{l}^{2}}}{12}$
$\Rightarrow {{I}_{1}}=\dfrac{m{{l}^{2}}}{12}+m{{\left( \dfrac{l}{2} \right)}^{2}}$
$\Rightarrow {{I}_{1}}=\dfrac{4m{{l}^{2}}}{12}=\dfrac{1}{3}m{{l}^{2}}$
For rod BC,
${{I}_{2}}={{I}_{BC}}+m{{d}^{2}}$
$\Rightarrow {{I}_{2}}=\dfrac{1}{3}m{{l}^{2}}$
For rod CD,
${{I}_{3}}={{I}_{CD}}+m{{d}^{2}}$
$\Rightarrow {{I}_{3}}=\dfrac{1}{3}m{{l}^{2}}$
For rod DA,
${{I}_{4}}={{I}_{DA}}+m{{d}^{2}}$
$\Rightarrow {{I}_{4}}=\dfrac{1}{3}m{{l}^{2}}$
Now the total moment of inertia along z-axis due to the frame is given by,
${{I}_{z}}={{I}_{1}}+{{I}_{2}}+{{I}_{3}}+{{I}_{4}}$
$\Rightarrow {{I}_{z}}=\dfrac{1}{3}m{{l}^{2}}+\dfrac{1}{3}m{{l}^{2}}+\dfrac{1}{3}m{{l}^{2}}+\dfrac{1}{3}m{{l}^{2}}$
$\Rightarrow {{I}_{z}}=4\times \dfrac{1}{3}m{{l}^{2}}$
$\Rightarrow {{I}_{z}}=\dfrac{4}{3}m{{l}^{2}}$
Hence, moment of inertia due to the square frame is given by,
${{I}_{z}}=\dfrac{4}{3}m{{l}^{2}}$
Hence, option D is the correct answer.

So, the correct answer is “Option D”.

Note: The moment of inertia of a 2-D object about an axis passing perpendicular from it is known to be equal to the sum of the Moment of inertias of the object about 2 mutually perpendicular axes lying in the plane of the object. That is,
${{I}_{Z}}={{I}_{X}}+{{I}_{Y}}$
The parallel axis theorem is applicable for any object without any restriction, while, perpendicular axes theorem is applicable only to planar bodies.