Question

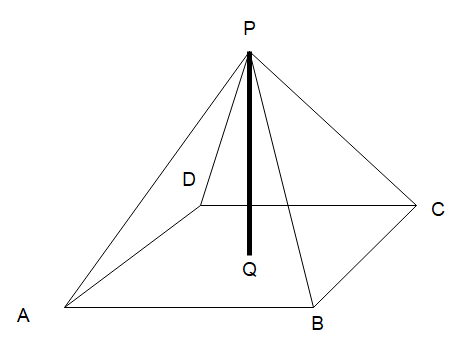
Four identical symmetrically located ideal inextensible strings (PA, PB, PC, and PD) support a rod PQ of mass $m$ in a vertical position as shown in the figure. The angle between two consecutive strings is equal to $60^\circ$ . Determine the normal force on the PQ given by the ground assuming that the tension in each string is $\sqrt 2 mg$ Newton (ABCD is a square on the ground):

A) $mg$
B) $2mg$
C) $3mg$
D) None

Answer 1

Hint : In this solution, we will calculate the force acted by the strings on the rod first. Since all the string’s force will also be downwards, the normal force will be determined by the sum of the weight of the rod and the net tension exerted by the spring.

Complete step by step answer:
In the diagram given to us, we’ve been told that all the strings are identical and symmetrically located which implies that all the strings will have an equal tension in the string as well as they will form the same angle with the rod. Let this angle be denoted by $\alpha$ .
Then we can determine $\alpha$ by calculating the sine of the angle $\angle APQ$ . The length of the side AQ will be half of the length of the diagonal of the square. If the length of the square is $a$ , the length of AQ $= \,a/\sqrt 2$ . Then the sine of the angle $\alpha$ is
$\sin \alpha = \dfrac{{AQ}}{{AP}}$
$\Rightarrow \sin \alpha = \dfrac{{a/\sqrt 2 }}{a}$
Which gives us
$\alpha = 45^\circ$
All the strings will exert force on the rod such that the rod exerts the net force of the string downwards. Then the net force acted by the rod on the square block will be the sum of the tension of all the strings which will only have a net vertical component and the weight of the rod:
$F = 4T\cos \alpha + mg$
$\Rightarrow F = 4\left( {\sqrt 2 mg} \right)\dfrac{1}{{\sqrt 2 }} + mg$
Which gives us the net force and hence the net normal force as
$F = 5mg$ which corresponds to none of the option so the correct choice is option (D).

Note:
The normal force will be equal to the net force acting on the square by the rod as the rod is stationary and so the pseudo-normal force will balance the applied force. If there was a net horizontal component of the resultant tension of the four strings, the rod would tip over and fall.