Question

Four identical rods each of mass M are joined to form a square frame, the moment of inertia of the system about one of the diagonals is
A. $\dfrac{{13M{l^2}}}{3}$
B. $\dfrac{{2M{l^2}}}{3}$
C. $\dfrac{{M{l^2}}}{6}$
D. $\dfrac{{13M{l^2}}}{6}$

Answer 1

Inertia of a body is its tendency to resist the change in its shape. The moment of inertia of a rotational system about an axis passing through its center is directly proportional to its mass if the body is moved away from the axis of its rotation. To solve the given question first of all we have to figure out the moment of inertia of the square frame about the axis passing through its center and perpendicular to its plane of rotation. Then after we will apply the perpendicular axis theorem in order to calculate the required moment of inertia of the system about one of the diagonals.

Complete step by step solution:
Let $l$ be the length of each side of the square frame, ω is the angular velocity
and $M$ is the mass of the rotating frame about the axis $XX’$ as shown in figure 1

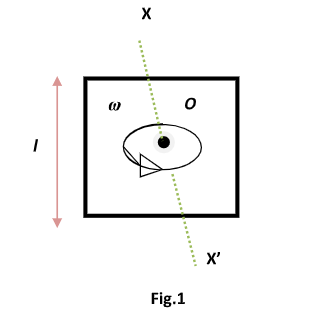
By using the parallel axis theorem (It states that: The moment of inertia of a body about any axis is equal to its moment of inertia about a parallel axis passes through its centre of mass plus product of mass of the body and the square of the distance between two the two axes) moment of inertia of the above frame can be calculated by simply adding the moment of inertia of each of the rod about the axis theorem passes through point O and perpendicular to the plane of rotation.
Therefore,
Moment of Inertia when the axis is perpendicular to the plane and passing through the centre of one of the rod is given by$= \dfrac{{M{l^2}}}{{12}}$
Step II:
Using parallel axis theorem to calculate the:

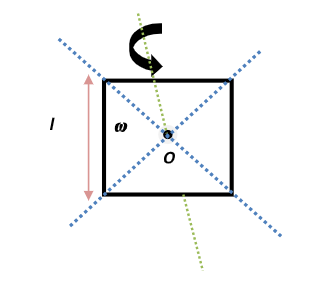
Moment of inertia of each about the point O is
$I = \dfrac{{M{l^2}}}{{12}} + M{r^2}$, (where we take $r = \dfrac{l}{2}$)
$= \dfrac{{M{l^2}}}{{12}} + M{\left( {\dfrac{l}{2}} \right)^2}$
$\Rightarrow I = \dfrac{{M{l^2}}}{3}$
Hence, Moment of inertia of each about the point O is
Step III:
Moment of Inertia of the whole system about the axis passing through O as:
$I' = 4I$
$I' = \dfrac{{4M{l^2}}}{3}$………….. (i)
Step IV:
Now, By using the perpendicular axis theorem:
Moment of Inertia of the whole system about one of the diagonals is
$I' = {I_x} + {I_y}$
$\Rightarrow I' = 2{I_x}$
$\Rightarrow {I_x} = \dfrac{{I'}}{2}$……………. (ii)
Substitute the value of $I'$from eqn (i) in the eqn (ii), we get
${I_x} = \dfrac{1}{2} \times \dfrac{{4M{l^2}}}{3}$
$\Rightarrow {I_x} = \dfrac{{2M{l^2}}}{3}$

$\therefore$ The moment of inertia of the system about one of the diagonals is ${I_x} = \dfrac{{2M{l^2}}}{3}$. Hence, option (B) is the correct answer.

Note:
Rotational inertia is the resistance offered by any system to the change in its rotation. It is a tensor which has different values at the different axis of rotation. In order to tackle such kinds of conceptual problems all we need to do is keep practicing a lot of questions on this topic and we should the role of mass distribution of mass in a rotating system and how it changes by changing the axis of rotation.