Question
Question: Four identical particles of mass \(M\)are located at the corners of a square of side \('a'\). What s...
Four identical particles of mass Mare located at the corners of a square of side ′a′. What should be their speed if each of them revolves under the influence of others gravitational field in a circular orbit circumscribing the square?
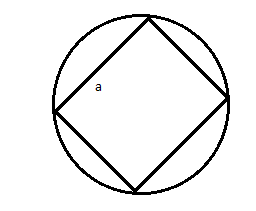
A.1.21aGM
B.1.41aGM
C.1.16aGM
D.1.35aGM
Solution
We should first draw the free body diagram of the given figure to solve the problem. Apply the equation for gravitation F=r2Gm1m2 after making the free body diagram to get the required solution. Idea of centripetal force is going to help in solving this. The force which is essential to keep the body moving in a curved path and it is directed towards the centre is called centripetal force.
Formula used:
We will use the following relations according to the free body diagram to get the required answer:-
F=Gr2m1.m2 and FC=rmv2
Complete step by step answer:
We have the diagram as
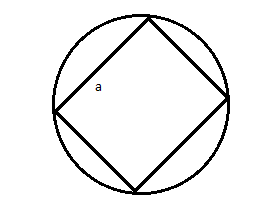
We will draw the free body diagram of the given figure in the problem as follows:-

$\dfrac{G{{M}^{2}}}{2{{a}^{2}}}$
In this diagram A, B, C and D are positions of particles of mass of M.
From the free body diagram made above and considering the basics of geometry, we can write the net force as follows:-
F=2a2GM2+a2GM22…………… (i)
Taking a2GM2common in(i), we get
F=a2GM2(21+2)……………….. (ii)
This force will be equal to the centripetal force from the centre of the circle. Distance from the centre of the circle is 2a(from the basics of geometry).
Therefore, the centripetal force from the centre is given as follows:-
FC=2aMv2…………… (iii)
But the forces in (ii)and (iii)must be equal.
So, F=FC
a2GM2(21+2)=2aMv2
Simplifying the equation, we get
aGM(221+1)=v2
Solving and simplifying further, we get
v2=aGM(1.35)
v=aGM1.16
v=1.16aGM
Hence, we get the correct option which is option(c).
Note: In these types of problems we should not be confused between centripetal force and centrifugal force. Basics of geometry regarding square and triangles are required to find out the distances between the given masses. Always try to start with a basic equation and then solve accordingly. We should draw the correct free body diagram.
