Question

Four identical mirrors are made to stand vertically to form a square arrangement as shown in a top view. A ray starts from the midpoint M of mirror AD and after two reflections reaches corner D. Then, angle $\theta$ must be:

A. ${\tan ^{ - 1}}\left( {0.75} \right)$
B. ${\cot ^{ - 1}}\left( {0.75} \right)$
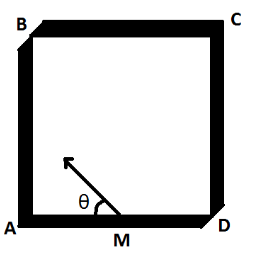
C. ${\sin ^{ - 1}}\left( {0.75} \right)$
D. ${\cos ^{ - 1}}\left( {0.75} \right)$

Answer 1

Here, we are given that a ray starts from the midpoint M of mirror AD and after two reflections reaches corner D. So our first step to solve this problem is to determine the angles of both the reflections with respective mirrors. After that, we will apply the trigonometric rules to get the required angle.

Complete step by step answer:
Let us consider that when ray starts from the midpoint M of mirror AD, it follows the path as shown in figure and after two reflections reaches corner D.

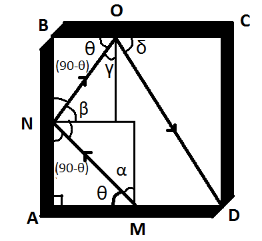
First, we will find the angles $\alpha$, $\beta$, $\gamma$ and $\delta$.
From the figure,
$\alpha = 90 - \theta$
$\Rightarrow\beta = 90 - \left( {90 - \theta } \right) = \theta$
$\Rightarrow\gamma = 90 - \beta = 90 - \theta$
$\Rightarrow\delta = 90 - \gamma = 90 - \left( {90 - \theta } \right) = \theta$
Now, or right angle triangle MAN,
$\tan \theta = \dfrac{{AN}}{{AM}} \\\ \Rightarrow AN = AM\tan \theta \\\$
Now if take the length of each mirror as $x$, then
$BN = x - AN \\\ \Rightarrow BN = x - AM\tan \theta \\\$
Now, from triangle NBO,
$\tan \theta = \dfrac{{BN}}{{BO}}$
In triangle OCD,
\tan \delta = \tan \theta = \dfrac{x}{{OC}} \\\ \Rightarrow \tan \theta = \dfrac{x}{{x - BO}} \\\ \Rightarrow \tan \theta = \dfrac{x}{{x - \dfrac{{\left( {x - \dfrac{x}{2}\tan \theta } \right)}}{{\tan \theta }}}} \\\ \Rightarrow \tan \theta = \dfrac{{x\tan \theta }}{{\dfrac{{3x}}{2}\tan \theta - x}} \\\
$\Rightarrow \tan \theta = \dfrac{{\tan \theta }}{{\dfrac{3}{2}\tan \theta - 1}}$
\Rightarrow \dfrac{3}{2}\tan \theta - 1 = 1 \\\ \Rightarrow \tan \theta = \dfrac{4}{3} \\\ \Rightarrow \cot \theta = \dfrac{3}{4} \\\ \Rightarrow \cot \theta = 0.75 \\\ \therefore \theta = {\cot ^{ - 1}}\left( {0.75} \right) \\\
Thus, the value of angle $\theta$ must be ${\cot ^{ - 1}}\left( {0.75} \right)$.

Hence, option B is the right answer.

Note: In this question, we need to be careful while determining reflection because one mistake can lead us to the wrong answer. Here, in this problem, we have applied two trigonometric rules. First, the tangent of any angle is given by the ration of its opposite side to its adjacent side. Second, the inverse of tangent is cotangent by which we have determined our final answer.